Compression Algorithm

本篇学习笔记参考《算法》四版第五章“数据压缩”部分。

概述

数据压缩模型

数据压缩的模型可以这样表示：

模型由两部分组成，压缩盒与展开盒。压缩盒将一个比特流B转化成压缩后的版本C(B)，展开盒能够将C(B)转化回B。
若用 |B| 表示比特流中比特的数量，则 μ = |C(B)|/|B| 称为压缩率，该值越小，表示压缩算法越高效。
这种模型叫做无损压缩模型——保证不丢失任何信息，即压缩和展开之后的比特流必须和原始的比特流完全相同。许多类型的文件都会用到无损压缩，例如数值数据或者可执行代码。

数据压缩算法的局限性

① 不存在能够压缩任意比特流的算法。也就是说通用性的数据压缩是不可能存在的。

这里可以用反证法来说明：假设存在一个能够压缩任意比特流的算法，那么也就可以用它来压缩它自己的输出以得到一段更短的比特流，循环反复直到比特流长度为0。显然能够将任意比特流的长度压缩至0是不可能的，所以不存在这样的压缩算法。

② 不可能找到最佳的压缩算法。也就是说最优数据压缩（找到能够产生给定字符串的最短程序）是一个不可判定的问题。

压缩一个文件最好的办法是找到创建这些数据的程序。我们处理的大多数数据都是由某种程序产生的。

一个简单的例子，比如下面这张包含100万个伪随机比特的图：

乍一看要压缩这张图似乎难以进行，但是如果你知道生成这张图的是下面这段代码，那么压缩就易如反掌了。

public class RandomBits{
    public static void main(String[] args){
        int x = 11111;
        for (int i = 0; i < 1000000; i++){
            x = x * 314159 + 218281;
            BinaryStdOut.write(x > 0);
        }
        BinaryStdOut.close();
    }
}

游程编码

算法原理

比特流中最简单的形式就是一长串重复的比特，比如下面这条40位长的字符串：
0000000000000001111111000000011111111111
该字符串包含15个0，7个1，然后又7个0，最后是11个1。因此我们可以将该比特字符编码为15，7，7，11。所有字符都是由交替出现的0和1组成，因此我们只需要将游程的长度进行编码就行了。因此我们可以得到一个16字节的字符串（15=1111,7=0111,11=1011）：
1111011101111011
压缩率 μ = 16/40 = 40%。

只有游程的长度大于将它们用二进制表示所需的长度时才能节省空间。

游程编码还可以用于位图的压缩。如下图所示，一个字符 “q” ，每行的右侧是该行的游程编码，因为每行的开始于结束都是0，所以每行的游程数量都是奇数。因为每一行的结束之后就是另一行的开始，所以比特流中相对应的游程长度就是每一行的最后一个游程长度和下一行的第一个游程长度之和。

算法实现

public static void expand() {
	boolean b = false;
	while (!BinaryStdIn.isEmpty()) {
		char cnt = BinaryStdIn.readChar();
		for (int i = 0; i < cnt; i++)
			BinaryStdOut.write(b);
		b = !b;
	}
	BinaryStdOut.close();
}

public static void compress(){
    char cnt = 0;
    boolean b, old = false;
    while (!BinaryStdIn.isEmpty()){
        b = BinaryStdIn.readBoolean();
        if (b != old){
            BinaryStdOut.write(cnt);
            cnt = 0;
            old = !old;
        }
        else{
            if (cnt == 255){
                BinaryStdOut.write(cnt);
                cnt = 0;
                BinaryStdOut.write(cnt);
            }
        }
    cnt++;
    }
    BinaryStdOut.write(cnt);
    BinaryStdOut.close();
}

expand()实现相对简单：读取一个游程的长度，将当前比特按照长度复制并打印，装换当前比特后继续，直到输入结束；
对于compress()方法，流程是这样的：

1、读取一个比特；
2、如果它和上一个比特不同，写入当前的计数值并将计数器归零；
3、如果它与上一个比特相同且计数器已经达到最大值，则写入计数值，再写入一个0计数值，然后将计数器归零；
4、增加计数器的值；
当输入流结束后，写入计数值（最后一个游程的长度）并结束。

游程编码在很多场景中非常有效，但是在许多情况下我们希望压缩的比特流并不含有较长的游程（例如典型的英文文档），这时我们需要用到另外的压缩算法。

霍夫曼压缩

前缀码

霍夫曼压缩算法是一种能够大幅压缩自然语言文件空间（以及许多其他类型文件）的数据压缩技术，它的主要思想就是放弃文本文件的普遍保存方式，不再使用7位或者8位二进制数表示每一个字符，而是用较少的比特表示出现频率高的字符，用较多的比特表示出现频率低的字符。

为了避免编码的二义性，引入了前缀码的概念，所谓的前缀码，就是所有字符编码都不会成为其他字符编码的前缀，这样的话就不需要使用分隔符来区分每一个字符编码。

表示前缀码的一种简便方法就是使用单词查找树。下图是字符串 BRACADABRA! 中字符的两种前缀编码方式。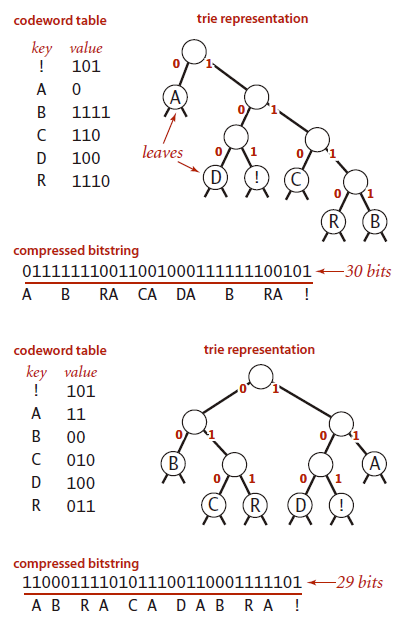

对于同一段字符串可以有很多种不同的前缀码编码，如何找到最优的前缀码呢？霍夫曼找到了这种通用方法，因此这种编码方式被称为霍夫曼编码。

原理

使用前缀码进行数据压缩需要经过5个主要步骤：

1、构造一棵编码单词查找树；
2、将该树以字节流的形式写入输出以供展开使用；
3、使用该树将字节流编码为比特流。

在展开式需要：

1、读取比特流开头的单词查找树；
2、使用该树将比特流解码。

算法实现

单词查找树节点表示：

private static class Node implements Comparable<Node>{ 
    // Huffman trie node
    private char ch; // unused for internal nodes
    private int freq; // unused for expand
    private final Node left, right;
    
    Node(char ch, int freq, Node left, Node right){
        this.ch = ch;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }
    public boolean isLeaf(){ 
        return left == null && right == null; 
    }
    public int compareTo(Node that){ 
        return this.freq - that.freq; 
    }
}

expend()代码：

public static void expand(){
    Node root = readTrie(); //读取单词查找树
    int N = BinaryStdIn.readInt();  //读取编码字符
    for (int i = 0; i < N; i++}{
        Node x = root;  //从树根节点开始
        while (!x.isLeaf()){
            if (BinaryStdIn.readBoolean()){
                 x = x.right;   //1则往右子数查找
            } else {
                x = x.left;    //0则往左子数查找
            }
        }
        BinaryStdOut.write(x.ch);   //输出编码对应字符
    }
    BinaryStdOut.close();
}

压缩时，使用单词查找树定义的编码来构造编译表。编译表就是一张将每个字符和它的比特字符串相关联的符号表。以下代码使用一个字符索引数组st[]作为符号表，在构造该符号表时，buildCode()递归遍历整棵树并为每个节点维护了一条从根节点到它的路径所对应的二进制字符串（0代表左链接，1代表右链接），每当到达一个叶子节点时，算法就将节点的编码设为该二进制字符串。

private static String[] buildCode(Node root){ 
    // 使用单词查找树构造编译表
    String[] st = new String[R];
    buildCode(st, root, "");
    return st;
}
private static void buildCode(String[] st, Node x, String s){
    if (x.isLeaf()){ st[x.ch] = s; return; }
    buildCode(st, x.left, s + '0');
    buildCode(st, x.right, s + '1');
}

//使用编译表压缩
for (int i = 0; i < input.length; i++){
    String code = st[input[i]];
    for (int j = 0; j < code.length(); j++)
    if (code.charAt(j) == '1')
    BinaryStdOut.write(true);
    else BinaryStdOut.write(false);
}

单词查找树的构造
构造单词查找树是一个构造最小生成树的过程。以以下字符串为例：

it was the best of times it was the worst of times

我们在每个结点中维护一个变量freq表示该字符出现的频率（要得到freq值，需要完整读取输出流一次）。构造的第一步就是创建一片由许多只有一个结点的树组成的森林，然后自底向上根据频率构造这棵单词查找树。构造过程如下：首先取得freq值最小的两棵树，然后创建以这两棵树为子结点的新结点，该结点freq值为其两个子结点之和，反复重复这个过程，最终只剩下一颗树，就是我们要的单词查找树。

private static Node buildTrie(int[] freq){
    //使用多棵单节点树初始化优先队列
    MinPQ<Node> pq = new MinPQ<Node>();
    for (char c = 0; c < R; c++)
        if (freq[c] > 0)
            pq.insert(new Node(c, freq[c], null, null));
    
    while (pq.size() > 1){ 
        // 合并两棵频率最小的树
        Node x = pq.delMin();
        Node y = pq.delMin();
        Node parent = new Node('\0', x.freq + y.freq, x, y);
        pq.insert(parent);
    }
    return pq.delMin();
}

构造过程图示如下：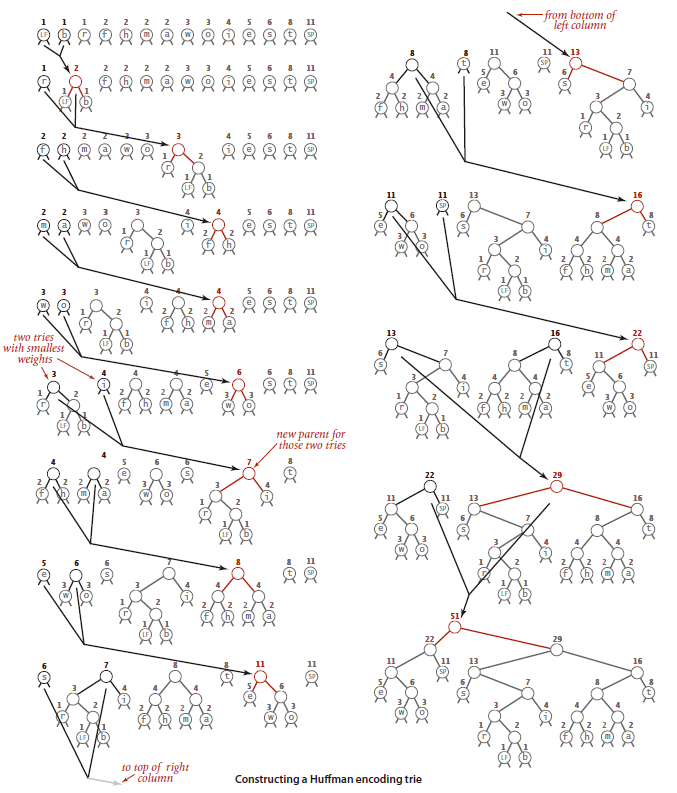

最终生成的单词查找树如下：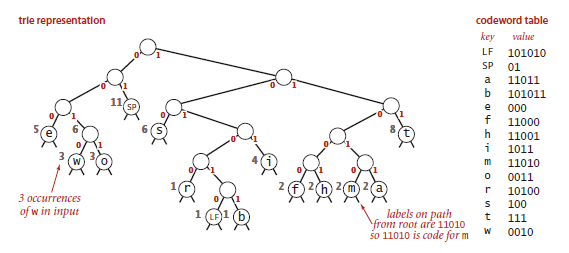

接下来需要解决的是写入和读取单词查找树。代码如下：

private static void writeTrie(Node x){ 
    //输出单词查找树的比特字符串
    if (x.isLeaf()){
        BinaryStdOut.write(true);
        BinaryStdOut.write(x.ch);
        return;
    }
    BinaryStdOut.write(false);
    writeTrie(x.left);
    writeTrie(x.right);
}
private static Node readTrie(){
    if (BinaryStdIn.readBoolean())
        return new Node(BinaryStdIn.readChar(), 0, null, null);
    return new Node('\0', 0, readTrie(), readTrie());
}

writeTree()过程是这样的：使用前序遍历单词查找树，当它访问的是一个内部结点是写入0；当它访问的是叶子结点时写入1，然后紧接着写入该叶子结点中字符的8位ASCII编码。
readTree()过程是这样的：首先读取一个比特得到当前结点的类型，如果是叶子结点就读取字符编码并创建一个叶子结点，如果是内部结点就创建一个内部结点并递归地继续构造它的左右子树。
以字符串 “ABRACADABRA!”为例，写入过程如下图：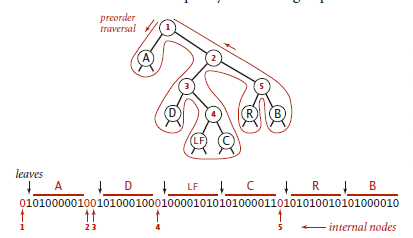

好，现在我们来完整地回顾一下霍夫曼编码的过程：

压缩过程
1、读取输入；
2、将输入中每个char值得出现频率制成表格；
3、根据频率构造相应的霍夫曼编码树；
4、构造编码表，将输入中的每个char值和一个比特字符相关联；
5、将单词查找树编码为比特字符串并写入输出流；
6、将单词总数编码为比特字符串并写入输出流；
7、使用编译表翻译每个输入字符。
解压过程
1、读取比特流开头的单词查找树；
2、读取需解码的字符数量；
3、使用单词查找树将比特流解码。

完整代码如下：

public class Huffman{
    private static int R = 256; // ASCII 字母表
    public static void compress(){
        // 读取输入
        String s = BinaryStdIn.readString();
        char[] input = s.toCharArray();
        // 统计频率
        int[] freq = new int[R];
        for (int i = 0; i < input.length; i++)
            freq[input[i]]++;
        // 构造霍夫曼编码树
        Node root = buildTrie(freq);
        // 递归地构造编码表
        String[] st = new String[R];
        buildCode(st, root, "");
        // 打印解码用的单词查找表
        writeTrie(root);
        // 打印字符总数
        BinaryStdOut.write(input.length);
        // 使用霍夫曼编码处理输入
        for (int i = 0; i < input.length; i++){
            String code = st[input[i]];
            for (int j = 0; j < code.length(); j++)
                if (code.charAt(j) == '1')
                    BinaryStdOut.write(true);
                else BinaryStdOut.write(false);
    }
    BinaryStdOut.close();
    }
}

LZW压缩

LZW压缩是由 A.Lempel、J.Ziv和T.Welch发明的一种算法，这种算法的基本思想和霍夫曼编码刚好相反。霍夫曼算法是输入中的定长模式产生一张变长的编码编译表，但是这种算法是为输入的变长模式生成一张定长的编码编译表。简单来说，这种压缩算法维护了一张（字符串：数字）的串表，将每个第一次出现的串放在一个串表中，用一个数字来表示串，压缩文件只存贮数字，则不存贮串，从而使文件的压缩效率得到较大的提高。奇妙的是，不管是在压缩还是在解压缩的过程中都能正确的建立这个串表，压缩或解压缩完成后，这个串表又被丢弃。

算法基本思想

LZW压缩算法有点难懂，我也是看了许久才发现其中的精妙之处……
在介绍基本思想之前，先说明几个名词：
字符：输入的字节
字符串：输入的字节序列
编码：输出的字节

这些名词在其它地方可能有其他含义，但是在LZW压缩中专指以上含义。

LZW算法的操作是这样的：
对于一串输入，确定其字符的种类，然后进行编码。一般对于ASCII码，在符号表中将128个单字符键的值初始化为8位编码，如果用16进制表示，则A的编码是41，R的编码是52等等。最后把80保留为文件结尾的标志，这样的话从 0-80 就都有使用了。如果接下来要对输入中遇到的各种子字符串进行编码，则从81开始递增。

只要输入还没有结束，则不断进行以下操作：
① 找出未处理的输入中在符号表中最长的前缀字符串s；
② 输出 s 的八位编码；
③ 继续扫描 s 之后的一个字符 c （前瞻字符）；
④ 在符号表中将 s+c (连接s和c)的值设置为下一个编码值。

大致流程如下图所示：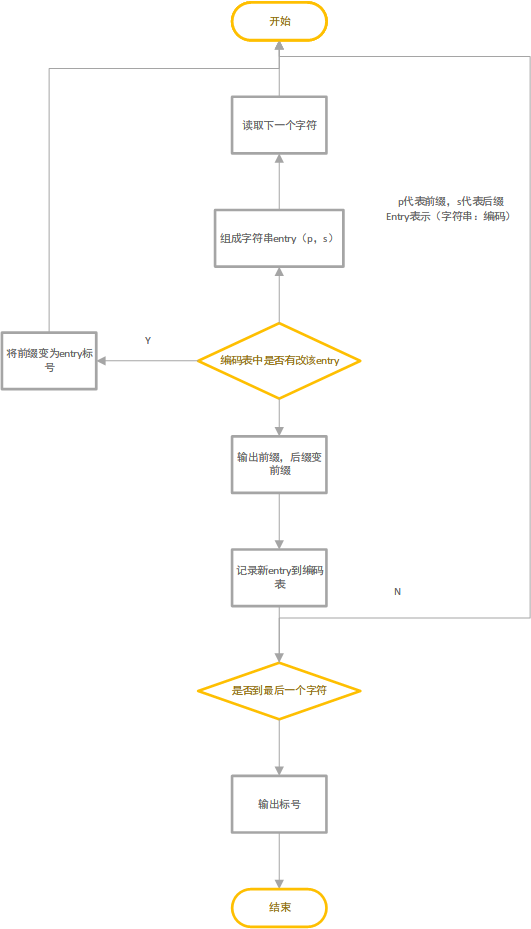

LZW压缩

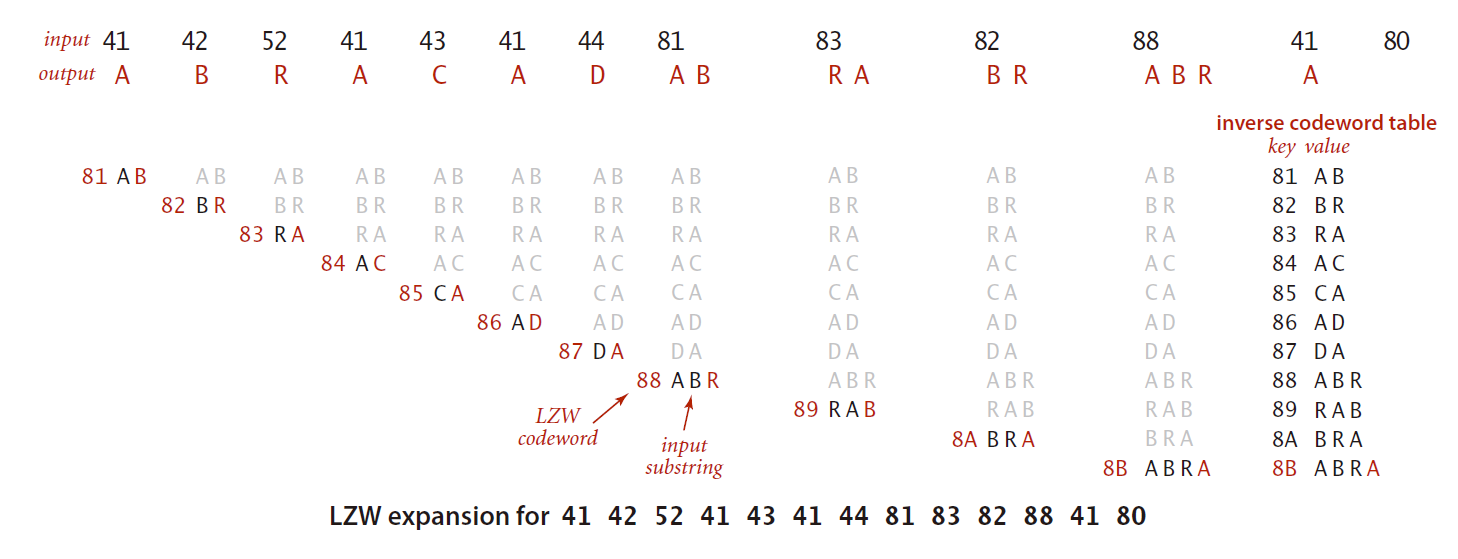
下图是对于输入 A B R A C A D AB RA BR ABR A 压缩的详细过程。
这里假设单字符集为ASCII所有字符，即对子字符串的编码从81开始。

从头开始扫描，一开始是最长前缀匹配是A，直接输出A的编码，此时扫描到(AB)，发现在编码表中没有该项，则把该项加入，即（AB:81）；接着将B作为前缀，最长匹配为B，直接输出B的编码，然后扫描到（BR），发现在编码表中没有该项，则把该项加入，即（BR:82）……以此类推可得到右边的编码表。
经过完整的过程，最终的压缩输出为：41(A) 42(B) 52(R) 41(A) 43(C) 41(A) 44(D) 81(AB) 83(RA) 82(BR) 88(ABR) 41(A) 80（end）
输入为17个7位ASCII字符，共119位；输出为13位八位编码，共104位——压缩比为87%。
LZW压缩的伪代码为：

STRING = get input character
WHILE there are still input characters DO
    CHARACTER = get input character
    IF STRING+CHARACTER is in the string table then
        STRING = STRING+character
    ELSE
        output the code for STRING
        add STRING+CHARACTER to the string table
        STRING = CHARACTER
    END of IF
END of WHILE
output the code for STRING 

LZW压缩的展开

在展开时，会维护一张关联字符串和编码值的符号表，这张表中加入了从00到7F和所有单个ASCII字符的字符串的关联条目，将第一个未关联的编码值设为81，将保留了当前字符串的变量val设为含有第一个字符的字符串，在遇到80之前不断进行如下操作：
① 输出当前字符串val
② 从输入中读取一个编码x
③ 在符号表中将s设为和x关联的值
④ 在符号表中将下一个未分配的编码值设为val+c，其中c为s的首字母
⑤ 将当前字符串val设为s

特殊情况
以上的操作有可能遇到处理不了的情况，考虑如下字符串：
A B AB ABA
被压缩得到的编码为：
41 42 81 83 80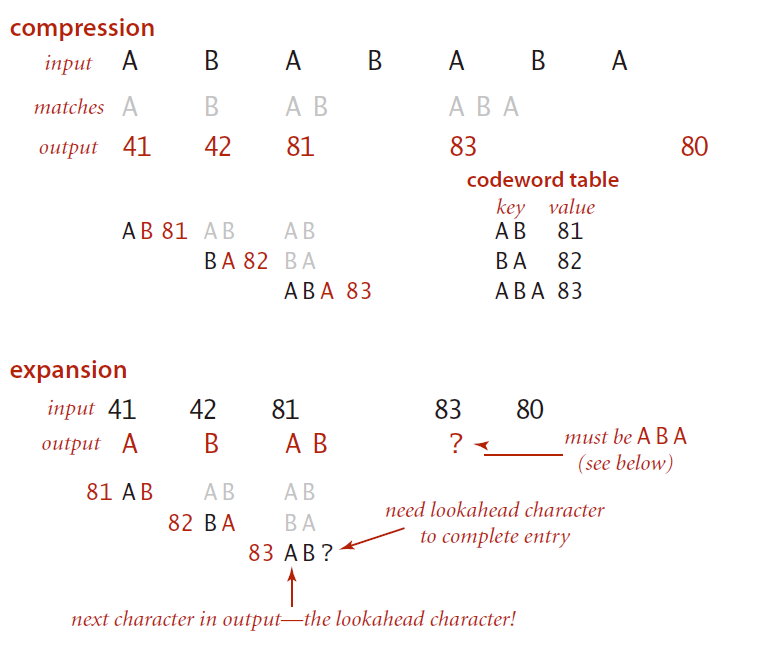

在展开时，首先得到编码41输出A，然后得到编码42得到前瞻字符并将（AB:81）插入符号表，输出B；读取81得到前瞻字符并将（BA:82）插入符号表，输出AB；到目前为止进展还不错，但接下来读取83并希望得到前瞻字符时发现此时要不全的符号表条目正是83，在这里就卡住了。幸运的是，检查（只有在读取的编码和需要完成的编码条目相同时才会出现）并修正（此时，前瞻字符必然是当前字符串的首字母，因为她就是下个将被输出的字符）这种情况并不难。在这个例子中，前瞻字符必然是A，因此，下一个被输出的字符串和符号表中83的值都是ABA。