Mooyu's Blog
0%

MXNet/Gluon 深度学习笔记 (三) —— 卷积神经网络模型整理

Posted on Edited on

在神经网络火起来之前，特征表示这步都是基于硬拼出来的直觉，机械化手工地生成。做出一组特征，改进结果，并把方法写出来是计算机视觉论文里的一个重要流派。

然而另一些人则认为特征本身是可以学习而来的，他们还相信，为了表征足够复杂的输入，特征本身应该阶级式地组合起来。持这一想法的研究者们，
包括 Yann LeCun，Geoff Hinton，Yoshua Bengio，Andrew Ng，Shun-ichi Amari，Juergen Schmidhuber，相信通过把许多神经网络层组合起来训练，
他们可能可以让网络学得阶级式的数据表征。在图片中，底层可以表示边，色彩和纹理。

网络提取的特征

高层可能可以基于这些表示，来表征更大的结构，如眼睛，鼻子，草叶和其他特征。更高层可能可以表征整个物体，如人，飞机，狗，飞盘。最终，在分类器层前的隐含层可能会表征经过汇总的内容，其中不同的类别将会是线性可分的。然而许多年来，研究者们由于缺乏大规模的数据，计算力不行等原因未能实现这一愿景。

这一状况直到 ImageNet 的出现以及现代计算机算力的迅速增长而改变，从而开启了深度学习的时代。本篇博文根据 MXNet/Gluon 的视频教程，整理了近些年曾“呼风唤雨”过的神经网络模型。

CNN 简介

卷积层

卷积神经网络是主要由卷积层构成的神经网络。卷积层跟全连接层类似，但输入和权重不是做简单的矩阵乘法，而是使用每次作用在一个窗口上的卷积。下图演示了输入是一个 5×5 矩阵，进行 1 单位的填充，使用一个 3×3 的权重，步长为 2，计算得到 3×3 结果的过程。每次采样一个跟权重一样大小的窗口，让它跟权重做按元素（element-wise）的乘法然后相加, 通常也把这个权重叫 kernel 或者 filter。

卷积操作示意图

当输入有多个通道时，每个通道都会有对应的权重，然后会对每个通道做卷积之后在通道之间求和

池化层

因为卷积层每次作用在一个窗口，它对位置很敏感。池化层能够很好的缓解这个问题。它跟卷积类似每次作用一个小窗口，然后选出窗口里面最大的元素，或者平均元素作为输出。

使用 Gluon 定义模型

下面是 leNet 的 Gluon 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
from mxnet.gluon import nn

net = nn.Sequential()
with net.name_scope():
    net.add(
        nn.Conv2D(channels=20, kernel_size=5, activation='relu'),
        nn.MaxPool2D(pool_size=2, strides=2),
        nn.Conv2D(channels=50, kernel_size=3, activation='relu'),
        nn.MaxPool2D(pool_size=2, strides=2),
        nn.Flatten(),
        nn.Dense(128, activation="relu"),
        nn.Dense(10)
    )

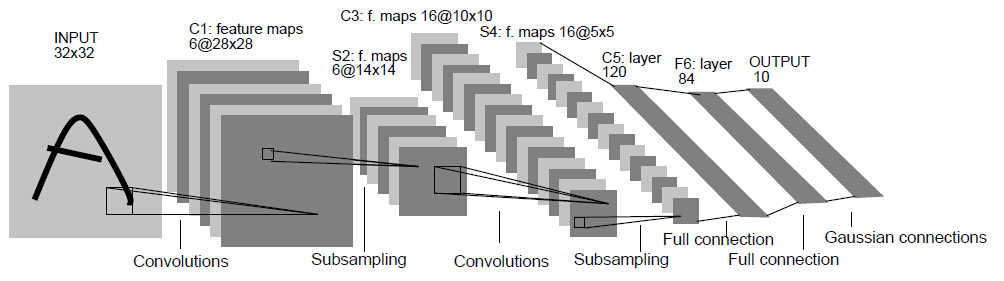
LeNet 模型结构

卷积操作示意图

AlexNet

2012年，Khrizhevsky，Sutskever 和 Hinton 凭借他们的 cuda-convnet 实现的 8 层卷积神经网络以很大的优势赢得了 ImageNet 2012 图像识别挑战。
他们在这篇论文中的模型与 1995 年的 LeNet 结构非常相似。

AlexNet 模型有一些显著的特征。第一，与相对较小的 LeNet 相比，AlexNet 包含 8 层变换，其中有五层卷积和两层全连接隐含层，以及一个输出层。

第一层中的卷积核大小是 11×11 ，接着第二层中的是 5×5，之后都是 3×3。此外，第一，第二和第五个卷积层之后都有重叠的大小为 3×3，步距为 2×2 的池化操作。

紧接着卷积层，原版的 AlexNet 有每层大小为 4096 个节点的全连接层。这两个巨大的全连接层带来将近 1GB 的模型大小。由于早期GPU显存的限制，最早的AlexNet包括了双数据流的设计，以让网络中一半的节点能存入一个GPU。这两个数据流，也就是说两个GPU只在一部分层进行通信，这样达到限制GPU同步时的额外开销的效果。幸运的是，GPU在过去几年得到了长足的发展，除了一些特殊的结构外，我们也就不再需要这样的特别设计了。

AlexNet 结构示意图

下面是用 Gluon 实现的简化版 AlexNet:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from mxnet.gluon import nn

net = nn.Sequential()
with net.name_scope():
    net.add(
        # 第一阶段
        nn.Conv2D(channels=96, kernel_size=11, strides=4, activation='relu'),
        nn.MaxPool2D(pool_size=3, strides=2),
        # 第二阶段
        nn.Conv2D(channels=256, kernel_size=5, padding=2, activation='relu'),
        nn.MaxPool2D(pool_size=3, strides=2),
        # 第三阶段
        nn.Conv2D(channels=384, kernel_size=3, padding=1, activation='relu'),
        nn.Conv2D(channels=384, kernel_size=3, padding=1, activation='relu'),
        nn.Conv2D(channels=256, kernel_size=3, padding=1, activation='relu'),
        nn.MaxPool2D(pool_size=3, strides=2),
        # 第四阶段
        nn.Flatten(),
        nn.Dense(4096, activation="relu"),
        nn.Dropout(.5),
        # 第五阶段
        nn.Dense(4096, activation="relu"),
        nn.Dropout(.5),
        # 第六阶段
        nn.Dense(10)
    )

从LeNet到Alexnet，虽然实现起来也就多了几行而已。但这个观念上的转变和真正跑出好实验结果，学术界整整花了20年。

VGG Net

VGG Net 全称 very deep convolutional networks。 顾名思义， VGG 比之前的网络都要深。此外，VGG 也是第一个在网络结构中使用大量重复结构的模型，这使得 VGG 的编程构造异常紧凑。VGG的一个关键是使用很多有着相对小的kernel（ 3×33×3 ）的卷积层然后接上一个池化层，之后再将这个模块重复多次。
以下是一个 VGG 块的定义

1
2
3
4
5
6
7
8
9
10
from mxnet.gluon import nn

def vgg_block(num_convs, channels):
    out = nn.Sequential()
    for _ in range(num_convs):
        out.add(
            nn.Conv2D(channels=channels, kernel_size=3, padding=1, activation='relu')
        )
    out.add(nn.MaxPool2D(pool_size=2, strides=2))
    return out

然后将这些块堆起来：
1
2
3
4
5
def vgg_stack(architecture):
  out = nn.Sequential()
  for (num_convs, channels) in architecture:
        out.add(vgg_block(num_convs, channels))
    return out

这里定义一个最简单的一个 VGG 结构，它有 8 个卷积层，和跟 Alexnet 一样的 3 个全连接层。这个网络又称 VGG 11. (更改不同的 architecture 就可以实现不同的 VGG)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
num_outputs = 10
architecture_vgg11 = ((1,64), (1,128), (2,256), (2,512), (2,512))
#architecture_vgg16 = ((2,64), (2,128), (3,256), (3,512), (3,512))
#architecture_vgg19 = ((2,64), (2,128), (4,256), (4,512), (4,512))
net = nn.Sequential()
# add name_scope on the outermost Sequential
with net.name_scope():
    net.add(
        vgg_stack(architecture_vgg11),
        nn.Flatten(),
        nn.Dense(4096, activation="relu"),
        nn.Dropout(.5),
        nn.Dense(4096, activation="relu"),
        nn.Dropout(.5),
        nn.Dense(num_outputs))

通过使用重复的元素，可以利用循环和函数来定义模型。使用不同的配置(architecture)可以得到一系列不同的模型。

论文中，作者提及的其他几种 VGG 的模型，如下表所示：

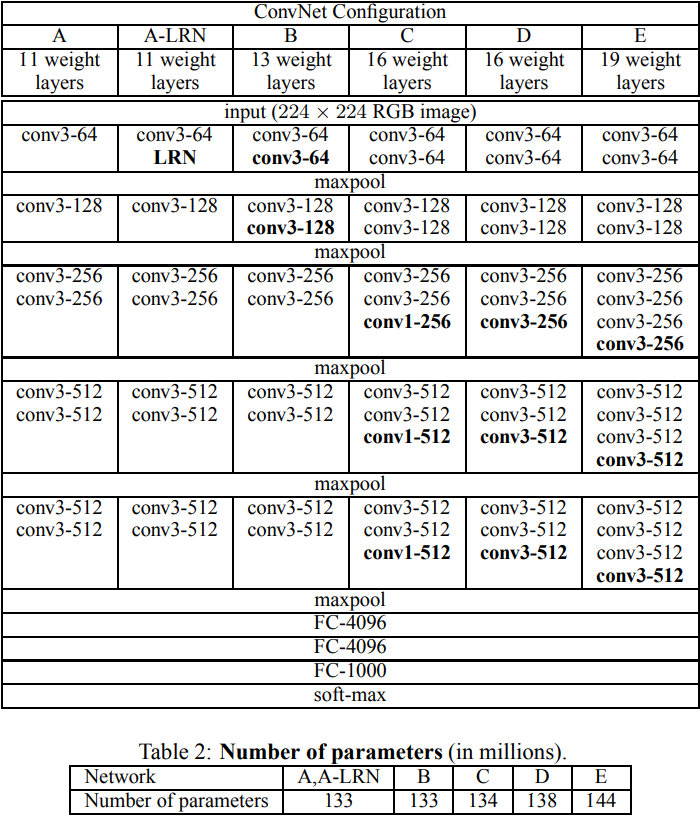
VGG 网络结构

Net in Net

Alexnet之后一个重要的工作是 Network in Network（NiN），这篇论文提出的两个想法影响了后面的网络设计。

这之前的神经网络结构一般分为两块，一块主要由卷积层构成，另一块主要是全连接层。在 Alexnet 里我们看到如何把卷积层块和全连接层分别加深加宽从而得到深度网络。另外一个自然的想法是，我们可以串联数个卷积层块和全连接层块来构建深度网络。

不过这里有个难题， 卷记得输入输出都是 4D 矩阵，然而全连接层是 2D 的。 如果将 4D 矩阵转成 2D 做全连接，则会导致全连接层有过多的参数。NiN 提出只对通道层做全连接并且像素之间共享权重来解决上述问题，也就是说，我们使用的 kernel 大小为 1x1 的卷积。

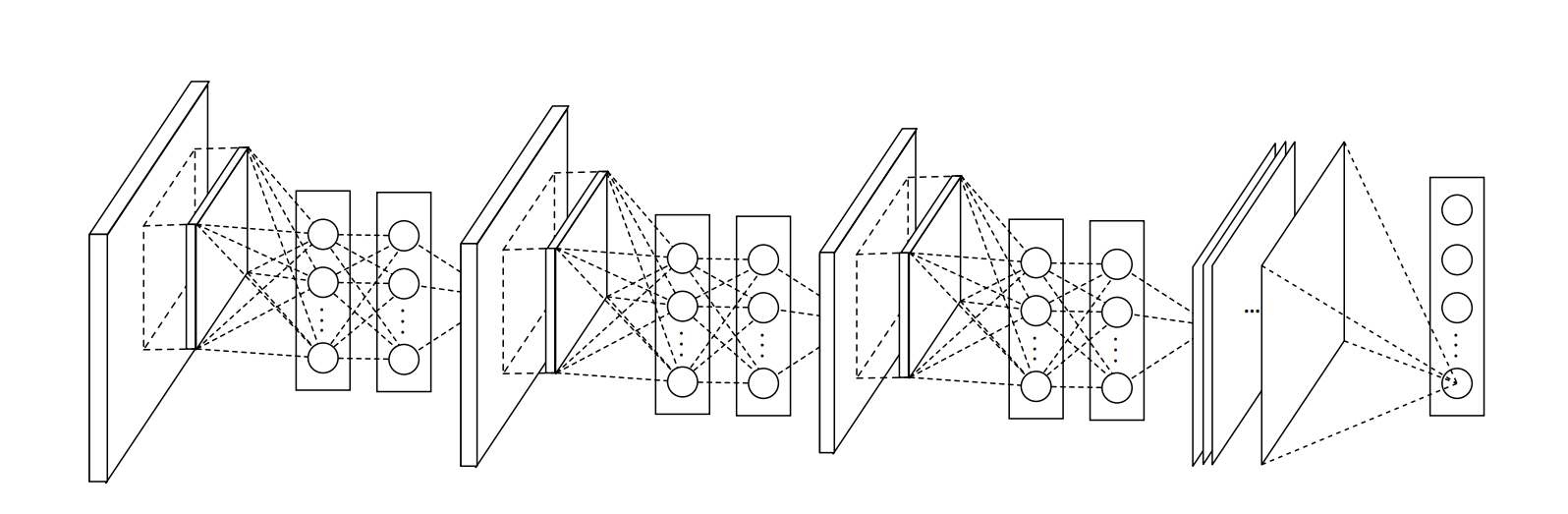
Network in Network

下面的代码定义了一个模块，它由一个正常的卷积层接上两个 kernel 为 1x1 的卷积层构成，后面两个卷积层充当了两个全连接的角色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from mxnet.gluon import nn

def mlpconv(channels, kernel_size, padding,
            strides=1, max_pooling=True):
    out = nn.Sequential()
    out.add(
        nn.Conv2D(channels=channels, kernel_size=kernel_size, strides=strides,
            padding=padding, activation='relu'),
        #充当全连接层
        nn.Conv2D(channels=channels, kernel_size=1, padding=0, strides=1, activation='relu'),
        nn.Conv2D(channels=channels, kernel_size=1, padding=0, strides=1, activation='relu'))
    if max_pooling:
        out.add(nn.MaxPool2D(pool_size=3, strides=2))
    return out

NiN 的卷积层的参数跟Alexnet类似，使用三组不同的设定

  • kernel: $11\times 11$, channels: 96
  • kernel: $5\times 5$, channels: 256
  • kernel: $3\times 3$, channels: 384

除了使用了$1\times 1$卷积外，NiN在最后不是使用全连接，而是使用通道数为输出类别个数的 mlpconv，外接一个平均池化层来将每个通道里的数值平均成一个标量。

平均池化层: 将每个通道里的数值平均成一个标量来代替全连接层，大大减少了计算量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
net = nn.Sequential()
# add name_scope on the outer most Sequential
with net.name_scope():
    net.add(
        mlpconv(96, 11, 0, strides=4),
        mlpconv(256, 5, 2),
        mlpconv(384, 3, 1),
        nn.Dropout(.5),
        # 目标类为10类
        mlpconv(10, 3, 1, max_pooling=False),
        # 输入为 batch_size x 10 x 5 x 5, 通过AvgPool2D转成
        # batch_size x 10 x 1 x 1。
        nn.AvgPool2D(pool_size=5),
        # 转成 batch_size x 10
        nn.Flatten()
    )

这种“一卷卷到底”最后加一个平均池化层的做法也成为了深度卷积神经网络的常用设计。

关于 1x1 卷积的理解

1x1卷积实际上是对每个像素点，在不同的 channels 上进行线性组合（信息整合），且保留了图片的原有平面结构，调控depth，从而完成升维或降维的功能。如下图所示，左边选择 2 个 filters 的 1x1 卷积，将原来的 depth = 3 降维为 2， 右边使用 4 个 filters 的 1x1 卷积， 将原来的 depth = 3 升维为 4。

1x1 卷积理解

图片来源：YJango的卷积神经网络——介绍

为什么mlpconv里面要有两个 1×1 卷积？

传统的卷积层可以看做一种广义的线性模型，如果提取到的特征线性可分，则传统的 CNN 对特征的抽象已经很充足了；但是，好的抽象特征一般需要对输入的数据做高低的非线性变换。因此以往的 CNN 有两个做法，一个是在同一层使用多个通道覆盖同一输入块（input data patch）特征的所有 variations (信息冗余，弥补了线性变换的不足)，另外就是多个卷积层的堆叠来获得比前层特征的更高抽象（特征抽象，同时获得更大的感受野）。这种操作会使得参数和计算量增加的太快。

因此，作者利用 1x1 的 kernel 来模拟这种操作，即实现了上述两个目的，又减少了参数的数量和计算量。
mlpconv 中第一个 1x1 的卷积层可以看做对前一层的所有 feature map 信息进行线性组合，可以看做一种在 channels 上的全连接层，再使用 Relu 进行非线性变换，就实现了一次特征的整合和非线性抽象。但是这与传统的卷积层没有什么区别，因此作者又加了一个同样的 1x1 卷积层，这样就实现了对输入数据进行高度的非线性变换的目的。

[From 网络中的网络 讨论区]

GoogLeNet

在 2014 年的 Imagenet 竞赛里，Google 的研究人员利用一个新的网络结构取得很大的优先。这个叫做 GoogLeNet 的网络虽然在名字上是向LeNet致敬，但网络结构里很难看到 LeNet 的影子。它颠覆的大家对卷积神经网络串联一系列层的固定做法。下图是其论文对 GoogLeNet 的可视化:

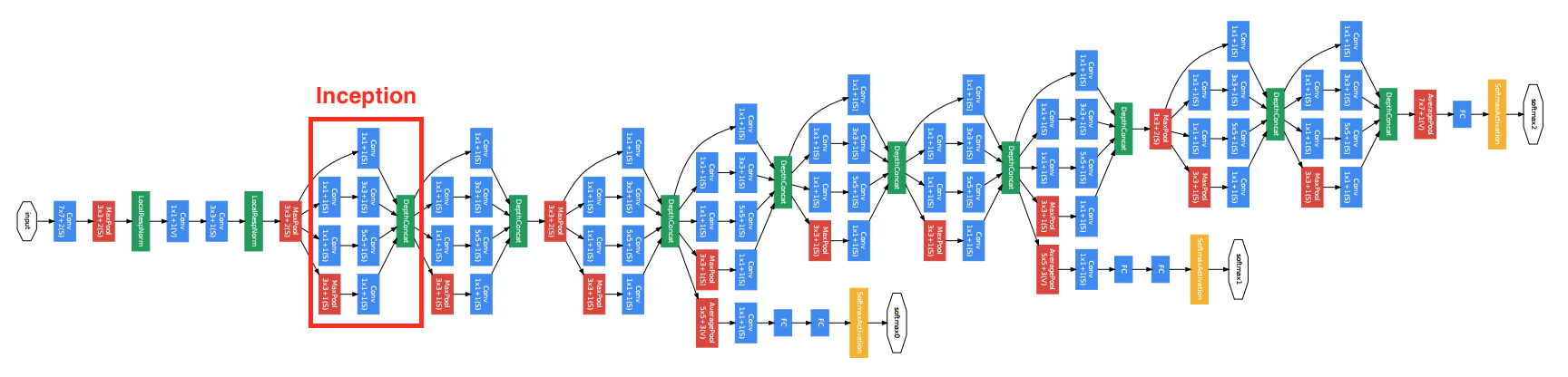
GoogLeNet

Inception

GoogLeNet 虽然复杂，但却有规可循。可以看到其结构有很多个四个并行卷积层的块，这个块一般叫做 Inception，它基于 NiN 的思想，当做了很大的改进。其结构如下图所示：

Inception

可以看到 Inception 里有四个并行的线路。

  1. 单个 $1\times 1$ 卷积。
  2. $1\times 1$ 卷积接上 $3\times 3$ 卷积。通常前者的通道数少于输入通道，这样减少后者的计算量。后者加上了padding=1使得输出的长宽的输入一致
  3. 同 2，但换成了 $5 \times 5$ 卷积
  4. 和 1 类似，但卷积前用了最大池化层

最后将这四个并行线路的结果在通道这个维度上合并在一起。

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from mxnet.gluon import nn
from mxnet import nd

class Inception(nn.Block):
    def __init__(self, n1_1, n2_1, n2_3, n3_1, n3_5, n4_1, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # path 1
        self.p1_conv_1 = nn.Conv2D(n1_1, kernel_size=1, activation='relu')
        # path 2
        self.p2_conv_1 = nn.Conv2D(n2_1, kernel_size=1, activation='relu')
        self.p2_conv_3 = nn.Conv2D(n2_3, kernel_size=3, padding=1, activation='relu')
        # path 3
        self.p3_conv_1 = nn.Conv2D(n3_1, kernel_size=1, activation='relu')
        self.p3_conv_5 = nn.Conv2D(n3_5, kernel_size=5, padding=2, activation='relu')
        # path 4
        self.p4_pool_3 = nn.MaxPool2D(pool_size=3, padding=1, strides=1)
        self.p4_conv_1 = nn.Conv2D(n4_1, kernel_size=1, activation='relu')

    def forward(self, x):
        p1 = self.p1_conv_1(x)
        p2 = self.p2_conv_3(self.p2_conv_1(x))
        p3 = self.p3_conv_5(self.p3_conv_1(x))
        p4 = self.p4_conv_1(self.p4_pool_3(x))
        return nd.concat(p1, p2, p3, p4, dim=1)

定义GoogLeNet

GoogLeNet将数个Inception串联在一起。注意到原论文里使用了多个输出，为了简化我们这里就使用一个输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class GoogLeNet(nn.Block):
    def __init__(self, num_classes, verbose=False, **kwargs):
        super(GoogLeNet, self).__init__(**kwargs)
        self.verbose = verbose
        # add name_scope on the outer most Sequential
        with self.name_scope():
            # block 1
            b1 = nn.Sequential()
            b1.add(
                nn.Conv2D(64, kernel_size=7, strides=2,
                          padding=3, activation='relu'),
                nn.MaxPool2D(pool_size=3, strides=2)
            )
            # block 2
            b2 = nn.Sequential()
            b2.add(
                nn.Conv2D(64, kernel_size=1),
                nn.Conv2D(192, kernel_size=3, padding=1),
                nn.MaxPool2D(pool_size=3, strides=2)
            )

            # block 3
            b3 = nn.Sequential()
            b3.add(
                Inception(64, 96, 128, 16,32, 32),
                Inception(128, 128, 192, 32, 96, 64),
                nn.MaxPool2D(pool_size=3, strides=2)
            )

            # block 4
            b4 = nn.Sequential()
            b4.add(
                Inception(192, 96, 208, 16, 48, 64),
                Inception(160, 112, 224, 24, 64, 64),
                Inception(128, 128, 256, 24, 64, 64),
                Inception(112, 144, 288, 32, 64, 64),
                Inception(256, 160, 320, 32, 128, 128),
                nn.MaxPool2D(pool_size=3, strides=2)
            )

            # block 5
            b5 = nn.Sequential()
            b5.add(
                Inception(256, 160, 320, 32, 128, 128),
                Inception(384, 192, 384, 48, 128, 128),
                nn.AvgPool2D(pool_size=2)
            )
            # block 6
            b6 = nn.Sequential()
            b6.add(
                nn.Flatten(),
                nn.Dense(num_classes)
            )
            # chain blocks together
            self.net = nn.Sequential()
            self.net.add(b1, b2, b3, b4, b5, b6)

    def forward(self, x):
        out = x
        for i, b in enumerate(self.net):
            out = b(out)
            if self.verbose:
                print('Block %d output: %s'%(i+1, out.shape))
        return out

GoogLeNet 加入了更加结构化的 Inception 块来使得我们可以使用更大的通道，更多的层，同时控制计算量和模型大小在合理范围内。

其他改进

GoogLeNet有数个后续版本

ResNet

当大家还在惊叹 GoogLeNet 用结构化的连接纳入了大量卷积层的时候，微软亚洲研究院的研究员已经在设计更深但结构更简单的网络ResNet。他们凭借这个网络在 2015 年的 Imagenet 竞赛中大获全胜。

ResNet 有效的解决了深度卷积神经网络难训练的问题。这是因为在误差逆向传播的过程中，梯度通常变得越来越小，从而权重的更新量也变小。这个导致远离损失函数的层训练缓慢，随着层数的增加这个现象更加明显。之前有两种常用方案来尝试解决这个问题：

  1. 按层训练。先训练靠近数据的层，然后慢慢的增加后面的层。但效果不是特别好，而且比较麻烦。
  2. 使用更宽的层（增加输出通道）而不是更深来增加模型复杂度。但更宽的模型经常不如更深的效果好。

ResNet 通过增加跨层的连接来解决梯度逐层回传时变小的问题。虽然这个想法之前就提出过了，但 ResNet 真正的把效果做好了。

下图演示了一个跨层的连接。

最底下那层的输入不仅仅是输出给了中间层，而且其与中间层结果相加进入最上层。这样在梯度逆向传播时，最上层梯度可以直接跳过中间层传到最下层，从而避免最下层梯度过小情况。

为什么叫做残差网络呢？我们可以将上面示意图里的结构拆成两个网络的和，一个一层，一个两层，最下面层是共享的。

在训练过程中，左边的网络因为更简单所以更容易训练。这个小网络没有拟合到的部分，或者说残差，则被右边的网络抓取住。所以直观上来说，即使加深网络，跨层连接仍然可以使得底层网络可以充分的训练，从而不会让训练更难。

Residual 块

ResNet 沿用了 VGG 的那种全用 $3\times 3$ 卷积，但在卷积和池化层之间加入了批量归一层来加速训练。每次跨层连接跨过两层卷积。这里我们定义一个这样的残差块。注意到如果输入的通道数和输出不一样时（same_shape=False），我们使用一个额外的 $1\times 1$ 卷积来做通道变化，同时使用strides=2来把长宽减半。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from mxnet.gluon import nn
from mxnet import nd

class Residual(nn.Block):
    def __init__(self, channels, same_shape=True, **kwargs):
        super(Residual, self).__init__(**kwargs)
        self.same_shape = same_shape
        strides = 1 if same_shape else 2
        self.conv1 = nn.Conv2D(channels, kernel_size=3, padding=1, strides=strides)
        self.bn1 = nn.BatchNorm()
        self.conv2 = nn.Conv2D(channels, kernel_size=3, padding=1)
        self.bn2 = nn.BatchNorm()
        if not same_shape:
            self.conv3 = nn.Conv2D(channels, kernel_size=1, strides=strides)

    def forward(self, x):
        out = nd.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        if not self.same_shape:
            x = self.conv3(x)
        return nd.relu(out + x)

构建ResNet

类似 GoogLeNet 主体是由 Inception 块串联而成，ResNet 的主体部分串联多个 Residual 块。下面定义 18 层的 ResNet。另外注意到一点是，这里没用池化层来减小数据长宽，而是通过有通道变化的 Residual 块里面的使用strides=2的卷积层。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class ResNet(nn.Block):
    def __init__(self, num_classes, verbose=False, **kwargs):
        super(ResNet, self).__init__(**kwargs)
        self.verbose = verbose
        # add name_scope on the outermost Sequential
        with self.name_scope():
            # block 1
            b1 = nn.Conv2D(64, kernel_size=7, strides=2)
            # block 2
            b2 = nn.Sequential()
            b2.add(
                nn.MaxPool2D(pool_size=3, strides=2),
                Residual(64),
                Residual(64)
            )
            # block 3
            b3 = nn.Sequential()
            b3.add(
                Residual(128, same_shape=False),
                Residual(128)
            )
            # block 4
            b4 = nn.Sequential()
            b4.add(
                Residual(256, same_shape=False),
                Residual(256)
            )
            # block 5
            b5 = nn.Sequential()
            b5.add(
                Residual(512, same_shape=False),
                Residual(512)
            )
            # block 6
            b6 = nn.Sequential()
            b6.add(
                nn.AvgPool2D(pool_size=3),
                nn.Dense(num_classes)
            )
            # chain all blocks together
            self.net = nn.Sequential()
            self.net.add(b1, b2, b3, b4, b5, b6)

    def forward(self, x):
        out = x
        for i, b in enumerate(self.net):
            out = b(out)
            if self.verbose:
                print('Block %d output: %s'%(i+1, out.shape))
        return out

ResNet使用跨层通道使得训练非常深的卷积神经网络成为可能。同样它使用很简单的卷积层配置，使得其拓展更加简单。

DenseNet

ResNet的跨层连接思想影响了接下来的众多工作。这里我们介绍其中的一个：DenseNet。下图展示了这两个的主要区别：

可以看到 DenseNet 里来自跳层的输出不是通过加法（+）而是拼接（concat）来跟目前层的输出合并。因为是拼接，所以底层的输出会保留的进入上面所有层。这是为什么叫“稠密连接”的原因。

稠密块（Dense Block）

DenseNet的卷积块使用ResNet改进版本的 BN->Relu->Conv。每个卷积的输出通道数被称之为 growth_rate，这是因为假设输入为 in_channels，而且有 layers 层，那么输出的通道数就是 in_channels + growth_rate * layers。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from mxnet import nd
from mxnet.gluon import nn

def conv_block(channels):
    out = nn.Sequential()
    out.add(
        nn.BatchNorm(),
        nn.Activation('relu'),
        nn.Conv2D(channels, kernel_size=3, padding=1)
    )
    return out

class DenseBlock(nn.Block):
    def __init__(self, layers, growth_rate, **kwargs):
        super(DenseBlock, self).__init__(**kwargs)
        self.net = nn.Sequential()
        for i in range(layers):
            self.net.add(conv_block(growth_rate))

    def forward(self, x):
        for layer in self.net:
            out = layer(x)
            x = nd.concat(x, out, dim=1)
        return x

过渡块（Transition Block）

因为使用拼接的缘故，每经过一次拼接输出通道数可能会激增。为了控制模型复杂度，这里引入一个过渡块，它不仅把输入的长宽减半，同时也使用 $1\times1$ 卷积来改变通道数。

1
2
3
4
5
6
7
8
9
def transition_block(channels):
    out = nn.Sequential()
    out.add(
        nn.BatchNorm(),
        nn.Activation('relu'),
        nn.Conv2D(channels, kernel_size=1),
        nn.AvgPool2D(pool_size=2, strides=2)
    )
    return out

DenseNet 实现

DenseNet 的主体就是交替串联稠密块和过渡块。它使用全局的 growth_rate 使得配置更加简单。过渡层每次都将通道数减半。下面定义一个 121 层的 DenseNet。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
init_channels = 64
growth_rate = 32
block_layers = [6, 12, 24, 16]
num_classes = 10

def dense_net():
    net = nn.Sequential()
    # add name_scope on the outermost Sequential
    with net.name_scope():
        # first block
        net.add(
            nn.Conv2D(init_channels, kernel_size=7, strides=2, padding=3),
            nn.BatchNorm(),
            nn.Activation('relu'),
            nn.MaxPool2D(pool_size=3, strides=2, padding=1)
        )
        # dense blocks
        channels = init_channels
        for i, layers in enumerate(block_layers):
            net.add(DenseBlock(layers, growth_rate))
            channels += layers * growth_rate
            if i != len(block_layers)-1:
                net.add(transition_block(channels//2))
        # last block
        net.add(
            nn.BatchNorm(),
            nn.Activation('relu'),
            nn.AvgPool2D(pool_size=1),
            nn.Flatten(),
            nn.Dense(num_classes)
        )
    return net