MXNet/Gluon 深度学习笔记 (四) —— 优化算法

优化算法对于深度学习十分重要。首先，实际中训练一个复杂的深度学习模型可能需要数小时、数日、甚至数周时间。而优化算法的效率直接影响模型训练效率。其次，深刻理解各种优化算法的原理以及其中各参数的意义将可以有助于我们更有针对性地调参，从而使深度学习模型表现地更好。

本篇博文详细介绍深度学习中一些常用的优化算法。

在一个机器学习的问题中，我们会预先定义一个损失函数，然后用优化算法来最小化这个损失函数。在优化中，这样的损失函数通常被称作优化问题的目标函数。依据惯例，优化算法通常只考虑最小化目标函数。任何最大化问题都可以很容易地转化为最小化问题：我们只需把目标函数前面的符号翻转一下。

在机器学习中，优化算法的目标函数通常是一个基于训练数据集的损失函数。因此，优化往往对应降低训练误差。而机器学习的主要目标在于降低泛化误差，例如应用一些应对过拟合的技巧。在本文中，我们只关注优化算法在最小化目标函数上的表现。

SGD

一维梯度下降

我们先以简单的一维梯度下降为例，解释梯度下降算法可以降低目标函数值的原因。一维梯度是一个标量，也称导数。

假设函数 $f: \mathbb{R} \rightarrow \mathbb{R}$ 的输入和输出都是标量。根据泰勒展开公式，我们得到

$$f(x + \epsilon) \approx f(x) + f'(x) \epsilon$$

假设 $\eta$ 是一个常数，将 $\epsilon$ 替换为 $-\eta f’(x)$ 后，我们有

$$f(x - \eta f'(x)) \approx f(x) - \eta f'(x)^2$$

如果 $\eta$ 是一个很小的正数，那么

$$f(x - \eta f'(x)) \leq f(x)$$

也就是说，如果当前导数 $f’(x) \neq 0$，按照 $x := x - \eta f’(x)$ 更新 $x$ 可能降低 $f(x)$ 的值。

由于导数 $f’(x)$ 是梯度在一维空间的特殊情况，上述更新 $x$ 的方法也即一维空间的梯度下降。一维空间的梯度下降如下图所示，参数 $x$ 沿着梯度方向不断更新。

学习率

上述梯度下降算法中的 $\eta$（取正数）叫做学习率或步长。需要注意的是，学习率过大可能会造成 $x$ 迈过（overshoot）最优解，甚至不断发散而无法收敛，如下图所示。

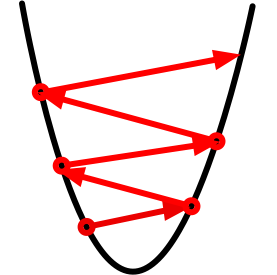
然而，如果学习率过小，优化算法收敛速度会过慢。实际中，一个合适的学习率通常是需要通过实验调出来的。

多维梯度下降

现在我们考虑一个更广义的情况：目标函数的输入为向量，输出为标量。

假设目标函数 $f: \mathbb{R}^d \rightarrow \mathbb{R}$ 的输入是一个多维向量 $\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$。目标函数 $f(\mathbf{x})$ 有关 $\mathbf{x}$ 的梯度是一个由偏导数组成的向量：

$$\nabla_\mathbf{x} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top.$$

为表示简洁，我们有时用 $\nabla f(\mathbf{x})$ 代替 $\nabla_\mathbf{x} f(\mathbf{x})$。梯度中每个偏导数元素 $\partial f(\mathbf{x})/\partial x_i$ 代表着$f$在 $\mathbf{x}$ 有关输入 $x_i$ 的变化率。为了测量 $f$ 沿着单位向量 $\mathbf{u}$ 方向上的变化率，在多元微积分中，我们定义 $f$ 在 $\mathbf{x}$ 上沿着 $\mathbf{u}$ 方向的方向导数为

$$D_\mathbf{u} f(\mathbf{x}) = \lim_{h \rightarrow 0} \frac{f(\mathbf{x} + h \mathbf{u}) - f(\mathbf{x})}{h}$$

由链式法则，该方向导数可以改写为

$$D_\mathbf{u} f(\mathbf{x}) = \nabla f(\mathbf{x}) \cdot \mathbf{u}$$

方向导数 $D_\mathbf{u} f(\mathbf{x})$ 给出了 $f$ 在 $\mathbf{x}$ 上沿着所有可能方向的变化率。为了最小化 $f$，我们希望找到 $f$ 能被降低最快的方向。因此，我们可以通过 $\mathbf{u}$ 来最小化方向导数 $D_\mathbf{u} f(\mathbf{x})$。

由于 $D_\mathbf{u} f(\mathbf{x}) = |\nabla f(\mathbf{x})| \cdot |\mathbf{u}| \cdot \text{cos} (\theta) = |\nabla f(\mathbf{x})| \cdot \text{cos} (\theta)$，其中 $\theta$ 为 $\nabla f(\mathbf{x})$ 和 $\mathbf{u}$ 之间的夹角，当 $\theta = \pi$，$\text{cos}(\theta)$ 取得最小值-1。因此，当 $\mathbf{u}$ 在梯度方向 $\nabla f(\mathbf{x})$ 的相反方向时，方向导数 $D_\mathbf{u} f(\mathbf{x})$ 被最小化。所以，我们可能通过下面的梯度下降算法来不断降低目标函数 $f$ 的值：

$$\mathbf{x} := \mathbf{x} - \eta \nabla f(\mathbf{x})$$

相同地，其中 $\eta$（取正数）称作学习率或步长。

随机梯度下降

然而，当训练数据集很大时，梯度下降算法可能会难以使用。为了解释这个问题，考虑目标函数

$$f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{x}),$$

其中 $f_i(\mathbf{x})$ 是有关索引为 $i$ 的训练数据点的损失函数。需要强调的是，梯度下降每次迭代的计算开销随着 $n$ 线性增长。因此，当 $n$ 很大时，每次迭代的计算开销很高。

这时我们需要随机梯度下降算法。在每次迭代时，该算法随机均匀采样 $i$ 并计算 $\nabla f_i(\mathbf{x})$。事实上，随机梯度 $\nabla f_i(\mathbf{x})$ 是对梯度 $\nabla f(\mathbf{x})$ 的无偏估计：

$$\mathbb{E}_i \nabla f_i(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}) = \nabla f(\mathbf{x})$$

小批量随机梯度下降

广义上，每次迭代可以随机均匀采样一个由训练数据点索引所组成的小批量 $\mathcal{B}$ 。类似地，我们可以使用

$$\nabla f_\mathcal{B}(\mathbf{x}) = \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\nabla f_i(\mathbf{x})$$

来更新 $\mathbf{x}$：

$$\mathbf{x} := \mathbf{x} - \eta \nabla f_\mathcal{B}(\mathbf{x}),$$

其中 $|\mathcal{B}|$ 代表批量中索引数量，$\eta$（取正数）称作学习率或步长。同样，小批量随机梯度 $\nabla f_\mathcal{B}(\mathbf{x})$ 也是对梯度 $\nabla f(\mathbf{x})$ 的无偏估计:

$$\mathbb{E}_\mathcal{B} \nabla f_\mathcal{B}(\mathbf{x}) = \nabla f(\mathbf{x}).$$

这个算法叫做小批量随机梯度下降。该算法每次迭代的计算开销为 $\mathcal{O}(|\mathcal{B}|)$。因此，当批量较小时，每次迭代的计算开销也较小。

SGD 的算法实现

这里只需要实现小批量随机梯度下降。当批量大小等于训练集大小时，该算法即为梯度下降；批量大小为1即为随机梯度下降。

# 小批量随机梯度下降
def sgd(params, lr, batch_size):
    for param in params:
        param[:] = param - lr * param.grad / batch_size

Momentum

在梯度下降算法中，每次迭代时，该算法沿着目标函数下降最快的方向更新参数。因此，梯度下降有时也叫做最陡下降（steepest descent）。在梯度下降中，每次更新参数的方向仅仅取决当前位置，这可能会带来一些问题。

考虑一个输入为二维向量 $\mathbf{x} = [x_1, x_2]^\top$，输出为标量的目标函数 $f: \mathbb{R}^2 \rightarrow \mathbb{R}$ 。下面为该函数的等高线示意图（每条等高线表示相同函数值的点：越靠近中间函数值越小）。

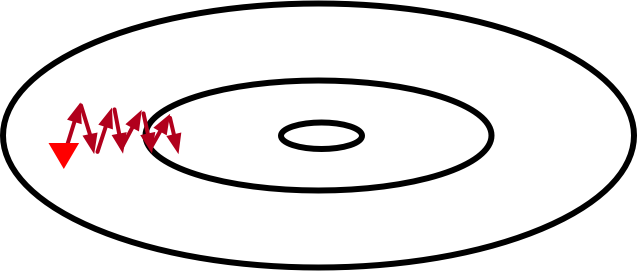
上图中，红色三角形代表参数 $\mathbf{x}$ 的初始值。带箭头的线段表示每次迭代时参数的更新。由于目标函数在竖直方向（ $x_2$ 轴方向）上比在水平方向（ $x_1$ 轴方向）弯曲得更厉害，梯度下降迭代参数时会使参数在竖直方向比在水平方向移动更猛烈。因此，我们需要一个较小的学习率从而避免参数在竖直方向上 overshoot。这就造成了上图中参数向最优解移动速度的缓慢。

动量法

动量法的提出是为了应对梯度下降的上述问题。广义上，以小批量随机梯度下降为例，我们对小批量随机梯度算法做如下修改：

$$\begin{align\*} \mathbf{v} &:= \gamma \mathbf{v} + \eta \nabla f_\mathcal{B}(\mathbf{x}),\\ \mathbf{x} &:= \mathbf{x} - \mathbf{v}, \end{align\*}$$

其中 $\mathbf{v}$ 是当前速度，$\gamma$ 是动量参数。其余符号如学习率 $\eta$、有关小批量 $\mathcal{B}$ 的随机梯度 $\nabla f_\mathcal{B}(\mathbf{x})$ 和上一节定义一样。

当前速度 $\mathbf{v}$ 的更新可以理解为对 $[\eta / (1 - \gamma)] \nabla f_\mathcal{B}(\mathbf{x})$ 做指数加权移动平均。因此，动量法的每次迭代中，参数在各个方向上移动幅度不仅取决当前梯度，还取决过去各个梯度在各个方向上是否一致。当过去的所有梯度都在同一方向，例如都是水平向右，那么参数在水平向右的移动幅度最大。如果过去的梯度中在竖直方向上时上时下，那么参数在竖直方向的移动幅度将变小。这样，我们就可以使用较大的学习率，从而如下图收敛更快。

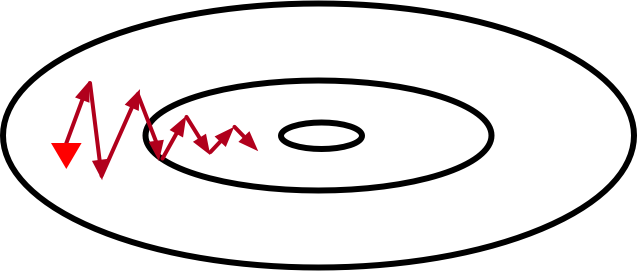
动量参数

为了有助于理解动量参数 $\gamma$，考虑一个简单的问题：每次迭代的小批量随机梯度 $\nabla f_\mathcal{B}(\mathbf{x})$ 都等于 $\mathbf{g}$ 。由于所有小批量随机梯度都在同一方向，动量法在该方向使参数移动加速：

$$\begin{align\*} \mathbf{v}_1 &:= \eta\mathbf{g},\\ \mathbf{v}_2 &:= \gamma \mathbf{v}_1 + \eta\mathbf{g} = \eta\mathbf{g} (\gamma + 1),\\ \mathbf{v}_3 &:= \gamma \mathbf{v}_2 + \eta\mathbf{g} = \eta\mathbf{g} (\gamma^2 + \gamma + 1),\\ &\ldots\\ \mathbf{v}_{\inf} &:= \frac{\eta\mathbf{g}}{1 - \gamma}. \end{align\*}$$

例如，当 $\gamma = 0.99$ , 最终的速度将是学习率乘以相应小批量随机梯度 $\eta\mathbf{g}$ 的100倍大。

实现

动量法的实现也很简单，在小批量随机梯度下降的基础上添加速度项

# 动量法。
def sgd_momentum(params, vs, lr, mom, batch_size):
    for param, v in zip(params, vs):
        v[:] = mom * v + lr * param.grad / batch_size
        param[:] -= v

Adagrad

在我们之前的优化算法中，无论是梯度下降、随机梯度下降、小批量随机梯度下降还是使用动量法，模型参数中的每一个元素在相同时刻都使用同一个学习率来自我迭代。

举个例子，当一个模型的损失函数为 $L$ ，参数为一个多维向量 $[x_1, x_2]^\top$ 时，该向量中每一个元素在更新时都使用相同的学习率，例如在学习率为 $\eta$ 的梯度下降中：

$$x_1 := x_1 - \eta \frac{\partial{L}}{\partial{x_1}} \\ x_2 := x_2 - \eta \frac{\partial{L}}{\partial{x_2}}$$

其中元素 $x_1$ 和 $x_2$ 都使用相同的学习率 $\eta$ 来自我迭代。如果让 $x_1$ 和 $x_2$ 使用不同的学习率自我迭代呢？

Adagrad 就是一个在迭代过程中不断自我调整学习率，并让模型参数中每个元素都使用不同学习率的优化算法。

算法详解

Adagrad 算法会使用一个梯度按元素平方的累加变量 $\mathbf{s}$，并将其中每个元素初始化为 0 。在每次迭代中，首先计算小批量梯度 $\mathbf{g}$ ，然后将该梯度按元素平方后累加到变量 $\mathbf{s}$：

$$\mathbf{s} := \mathbf{s} + \mathbf{g} \odot \mathbf{g}$$

然后将模型参数中每个元素的学习率通过按元素操作重新调整一下：

$$\mathbf{g}^\prime := \frac{\eta}{\sqrt{\mathbf{s} + \epsilon}} \odot \mathbf{g}$$

其中 $\eta$ 是初始学习率，$\epsilon$ 是为了维持数值稳定性而添加的常数，例如 $10^{-7}$。注意其中按元素开方、除法和乘法的操作，这些按元素操作使得模型参数中每个元素都分别拥有自己的学习率。

需要强调的是，由于梯度按元素平方的累加变量 $\mathbf{s}$ 出现在分母，Adagrad 的核心思想是：如果模型损失函数有关一个参数元素的偏导数一直都较大，那么就让它的学习率下降快一点；反之，如果模型损失函数有关一个参数元素的偏导数一直都较小，那么就让它的学习率下降慢一点。然而，由于 $\mathbf{s}$ 一直在累加按元素平方的梯度，每个元素的学习率在迭代过程中一直在降低或不变。所以在有些问题中，当学习率在迭代早期降得较快时且当前解依然不理想时，Adagrad 在迭代后期可能较难找到一个有用的解。

最后的参数迭代步骤与小批量随机梯度下降类似。只是这里梯度前的学习率已经被调整过了：

$$\mathbf{x} := \mathbf{x} - \mathbf{g}^\prime$$

算法实现

# Adagrad算法
def adagrad(params, sqrs, lr, batch_size):
    eps_stable = 1e-7
    for param, sqr in zip(params, sqrs):
        g = param.grad / batch_size
        sqr[:] += nd.square(g)
        div = lr * g / nd.sqrt(sqr + eps_stable)
        param[:] -= div

RMSProp

在 Adagrad 算法中，由于学习率分母上的变量 $\mathbf{s}$ 一直在累加按元素平方的梯度，每个元素的学习率在迭代过程中一直在降低或不变。所以在有些问题下，当学习率在迭代早期降得较快时且当前解依然不理想时，Adagrad 在迭代后期可能较难找到一个有用的解。

为了应对这一问题，RMSProp 算法对 Adagrad 做了一点小小的修改。

算法详情

RMSProp 算法会使用一个梯度按元素平方的指数加权移动平均变量 $\mathbf{s}$，并将其中每个元素初始化为 0 。在每次迭代中，首先计算小批量梯度 $\mathbf{g}$，然后对该梯度按元素平方后做指数加权移动平均并计算 $\mathbf{s}$：

$$\mathbf{s} := \gamma \mathbf{s} + (1 - \gamma) \mathbf{g} \odot \mathbf{g}$$

然后将模型参数中每个元素的学习率通过按元素操作重新调整一下：

$$\mathbf{g}^\prime := \frac{\eta}{\sqrt{\mathbf{s} + \epsilon}} \odot \mathbf{g}$$

其中 $\eta$ 是初始学习率，$\epsilon$ 是为了维持数值稳定性而添加的常数，例如 $10^{-8}$ 。和 Adagrad 一样，模型参数中每个元素都分别拥有自己的学习率。

同样地，最后的参数迭代步骤与小批量随机梯度下降类似，只是这里梯度前的学习率已经被调整过了：

$$\mathbf{x} := \mathbf{x} - \mathbf{g}^\prime$$

RMSProp 只在 Adagrad 的基础上修改了变量 $\mathbf{s}$ 的更新方法：把累加改成了指数加权移动平均。因此，每个元素的学习率在迭代过程中既可能降低又可能升高。

算法实现

# RMSProp
def rmsprop(params, sqrs, lr, gamma, batch_size):
    eps_stable = 1e-8
    for param, sqr in zip(params, sqrs):
        g = param.grad / batch_size
        sqr[:] = gamma * sqr + (1. - gamma) * nd.square(g)
        div = lr * g / nd.sqrt(sqr + eps_stable)
        param[:] -= div

Adadelta

Adadelta 和 RMSProp 类似，也是针对当学习率在迭代早期降得较快时且当前解依然不理想时 Adagrad 在迭代后期可能较难找到一个有用的解的解决方案，和 RMSProp 不同的是，Adadelta 没有学习率参数。

Adadelta 算法也像 RMSProp 一样使用了一个梯度按元素平方的指数加权移动平均变量 $\mathbf{s}$，并将其中每个元素初始化为 0 。在每次迭代中，首先计算小批量梯度 $\mathbf{g}$，然后对该梯度按元素平方后做指数加权移动平均并计算 $\mathbf{s}$：

$$\mathbf{s} := \rho \mathbf{s} + (1 - \rho) \mathbf{g} \odot \mathbf{g}$$

然后我们计算当前需要更新的参数的变化量：

$$\mathbf{g}^\prime = \frac{\sqrt{\Delta\mathbf{x} + \epsilon}}{\sqrt{\mathbf{s} + \epsilon}} \odot \mathbf{g}$$

其中 $\epsilon$ 是为了维持数值稳定性而添加的常数，例如 $10^{-5}$。和 Adagrad 一样，模型参数中每个元素都分别拥有自己的学习率。其中 $\Delta\mathbf{x}$ 初始化为零张量，并做如下 $\mathbf{g}^\prime$ 按元素平方的指数加权移动平均：

$$\Delta\mathbf{x} := \rho \Delta\mathbf{x} + (1 - \rho) \mathbf{g}^\prime \odot \mathbf{g}^\prime$$

同样地，最后的参数迭代步骤与小批量随机梯度下降类似。只是这里梯度前的学习率已经被调整过了：

$$\mathbf{x} := \mathbf{x} - \mathbf{g}^\prime$$

代码实现如下：

# Adadalta
def adadelta(params, sqrs, deltas, rho, batch_size):
    eps_stable = 1e-5
    for param, sqr, delta in zip(params, sqrs, deltas):
        g = param.grad / batch_size
        sqr[:] = rho * sqr + (1. - rho) * nd.square(g)
        cur_delta = nd.sqrt(delta + eps_stable) / nd.sqrt(sqr + eps_stable) * g
        delta[:] = rho * delta + (1. - rho) * cur_delta * cur_delta
        param[:] -= cur_delta

Adam

Adam 是一个组合了动量法和 RMSProp 的优化算法。

Adam 算法会使用一个动量变量 $\mathbf{v}$ 和一个 RMSProp 中梯度按元素平方的指数加权移动平均变量 $\mathbf{s}$，并将它们中每个元素初始化为 0。在每次迭代中，首先计算小批量梯度 $\mathbf{g}$，并递增迭代次数

$$t := t + 1$$

然后对梯度做指数加权移动平均并计算动量变量 $\mathbf{v}$:

$$\mathbf{v} := \beta_1 \mathbf{v} + (1 - \beta_1) \mathbf{g}$$

该梯度按元素平方后做指数加权移动平均并计算 $\mathbf{s}$：

$$\mathbf{s} := \beta_2 \mathbf{s} + (1 - \beta_2) \mathbf{g} \odot \mathbf{g}$$

在 Adam 算法里，为了减轻 $\mathbf{v}$ 和 $\mathbf{s}$ 被初始化为0在迭代初期对计算指数加权移动平均的影响（冷启动现象），算法做了如下的偏差修正：

$$\hat{\mathbf{v}} := \frac{\mathbf{v}}{1 - \beta_1^t}$$

和

$$\hat{\mathbf{s}} := \frac{\mathbf{s}}{1 - \beta_2^t}$$

可以看到，当 $0 \leq \beta_1, \beta_2 < 1$ 时（算法作者建议分别设为 0.9 和 0.999 ），当迭代后期$t$较大时，偏差修正几乎就不再有影响。我们使用以上偏差修正后的动量变量和 RMSProp 中梯度按元素平方的指数加权移动平均变量，将模型参数中每个元素的学习率通过按元素操作重新调整一下：

$$\mathbf{g}^\prime := \frac{\eta \hat{\mathbf{v}}}{\sqrt{\hat{\mathbf{s}} + \epsilon}}$$

其中 $\eta$ 是初始学习率，$\epsilon$ 是为了维持数值稳定性而添加的常数，例如 $10^{-8}$。和 Adagrad 一样，模型参数中每个元素都分别拥有自己的学习率。

同样地，最后的参数迭代步骤与小批量随机梯度下降类似。只是这里梯度前的学习率已经被调整过了：

$$\mathbf{x} := \mathbf{x} - \mathbf{g}^\prime$$

代码实现如下：

# Adam
def adam(params, vs, sqrs, lr, batch_size, t):
    beta1 = 0.9
    beta2 = 0.999
    eps_stable = 1e-8
    for param, v, sqr in zip(params, vs, sqrs):
        g = param.grad / batch_size
        v[:] = beta1 * v + (1. - beta1) * g
        sqr[:] = beta2 * sqr + (1. - beta2) * nd.square(g)
        v_bias_corr = v / (1. - beta1 ** t)
        sqr_bias_corr = sqr / (1. - beta2 ** t)
        div = lr * v_bias_corr / (nd.sqrt(sqr_bias_corr) + eps_stable)
        param[:] = param - div

总结

最后以一首打油诗总结：

梯度下降可沉甸， 随机降低方差难。

引入动量别弯慢， Adagrad梯方贪。

Adadelta学率换， RMSProp梯方权。

Adam动量RMS伴， 优化还需己调参。

注释：

• 梯方：梯度按元素平方
• 贪：因贪婪故而不断累加
• 学率：学习率
• 换：这个参数被换成别的了
• 权：指数加权移动平均