Mooyu's Blog
0%

MXNet/Gluon 深度学习笔记 (十一) —— seq2seq 和注意力机制

Posted on Edited on

在基于词语的语言模型中，我们使用了循环神经网络。它的输入是一段不定长的序列，输出却是定长的，例如一个词语。然而，很多问题的输出也是不定长的序列。以机器翻译为例，输入是可以是英语的一段话，输出可以是法语的一段话，输入和输出皆不定长，例如

英语：They are watching.

法语：Ils regardent.

当输入输出都是不定长序列时，我们可以使用编码器—解码器（encoder-decoder）或者 seq2seq。它们分别基于 2014 年的两个工作：

以上两个工作本质上都用到了两个循环神经网络，分别叫做编码器和解码器。编码器对应输入序列，解码器对应输出序列。

seq2seq 示意图:

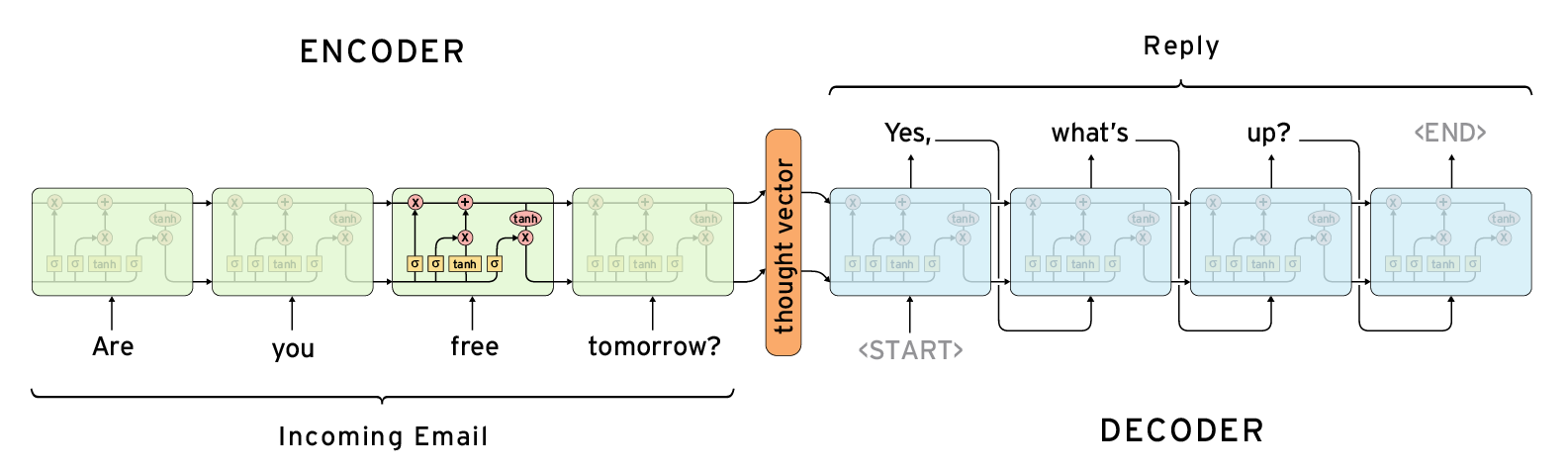
seq2seq

编码器—解码器

编码器和解码器是分别对应输入序列和输出序列的两个循环神经网络。我们通常会在输入序列和输出序列后面分别附上一个特殊字符 ‘<eos>’（end of sequence）表示序列的终止。在测试模型时，一旦输出 ‘<eos>’ 就终止当前的输出序列。

编码器

编码器的作用是把一个不定长的输入序列转化成一个定长的背景向量 $\mathbf{c}$ 。该背景向量包含了输入序列的信息。常用的编码器是循环神经网络。

假设循环神经网络单元为 $f$ ，在 $t$ 时刻的输入为 $x_t, t=1, \ldots, T$。
假设 $\mathbf{x}_t$ 是单个输出 $x_t$ 在嵌入层的结果，例如 $x_t$ 对应的 one-hot向量$\mathbf{o} \in \mathbb{R}^x$ 与嵌入层参数矩阵 $\mathbf{E} \in \mathbb{R}^{x \times h}$ 的乘积 $\mathbf{o}^\top \mathbf{E}$ 。隐含层变量

编码器的背景向量

一个简单的背景向量是该网络最终时刻的隐含层变量 $\mathbf{h}_T$, 我们将这里的循环神经网络叫做编码器。

双向循环神经网络

编码器的输入既可以是正向传递，也可以是反向传递。如果输入序列是 $x_1, x_2, \ldots, x_T$ ，在正向传递中，隐含层变量

而反向传递中，隐含层变量的计算变为

当希望编码器的输入既包含正向传递信息又包含反向传递信息时，可以使用双向循环神经网络。例如，给定输入序列 $x_1, x_2, \ldots, x_T$，按正向传递，它们在循环神经网络的隐含层变量分别是 $\overrightarrow{\mathbf{h}}_1, \overrightarrow{\mathbf{h}}_2, \ldots, \overrightarrow{\mathbf{h}}_T$；按反向传递，它们在循环神经网络的隐含层变量分别是 $\overleftarrow{\mathbf{h}}_1, \overleftarrow{\mathbf{h}}_2, \ldots, \overleftarrow{\mathbf{h}}_T$。在双向循环神经网络中，时刻 $i$ 的隐含层变量可以把 $\overrightarrow{\mathbf{h}}_i$ 和 $\overleftarrow{\mathbf{h}}_i$ 连结起来。

bi-rnn

基于 GRU 的编码器实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Encoder(Block):
    """编码器"""
    def __init__(self, input_dim, hidden_dim, num_layers, drop_prob):
        super(Encoder, self).__init__()
        with self.name_scope():
            self.embedding = nn.Embedding(input_dim, hidden_dim)
            self.dropout = nn.Dropout(drop_prob)
            self.rnn = rnn.GRU(hidden_dim, num_layers, dropout=drop_prob,
                               input_size=hidden_dim)

    def forward(self, inputs, state):
        # inputs尺寸: (1, num_steps, 256)，emb尺寸: (num_steps, 1, 256)
        emb = self.embedding(inputs).swapaxes(0, 1)
        emb = self.dropout(emb)
        output, state = self.rnn(emb, state)
        return output, state

    def begin_state(self, *args, **kwargs):
        return self.rnn.begin_state(*args, **kwargs)

解码器

编码器最终输出了一个背景向量 $\mathbf{c}$，该背景向量编码了输入序列 $x_1, x_2, \ldots, x_T$ 的信息。

假设训练数据中的输出序列是 $y_1, y_2, \ldots, y_{T^\prime}$ ，我们希望表示每个 $t$ 时刻输出的既取决于之前的输出又取决于背景向量。之后，我们就可以最大化输出序列的联合概率

并得到该输出序列的损失函数

为此，我们使用另一个循环神经网络作为解码器。解码器使用函数 $p$ 来表示单个输出 $y_{t^\prime}$ 的概率

其中的 $\mathbf{s}_t$ 为 $t^\prime$ 时刻的解码器的隐含层变量。该隐含层变量

其中函数 $g$ 是循环神经网络单元。

需要注意的是，编码器和解码器通常会使用多层循环神经网络。

注意力机制

在以上的解码器设计中，各个时刻使用了相同的背景向量, 如果解码器的不同时刻可以使用不同的背景向量呢？

以英语-法语翻译为例，给定一对输入序列 “they are watching” 和输出序列 “Ils regardent” ，解码器在时刻 1 可以使用更多编码了 “they are” 信息的背景向量来生成 “Ils”，而在时刻 2 可以使用更多编码了 “watching” 信息的背景向量来生成 “regardent”, 这看上去就像是在解码器的每一时刻对输入序列中不同时刻分配不同的注意力, 这也是注意力机制的由来。它最早由Bahanau等在2015年提出。

现在，对上面的解码器稍作修改。我们假设时刻 $t^\prime$ 的背景向量为 $\mathbf{c}_{t^\prime}$, 那么解码器在 $t^\prime$ 时刻的隐含层变量

令编码器在 $t$ 时刻的隐含变量为 $\mathbf{h}_t$ ，解码器在 $t^\prime$ 时刻的背景向量为

也就是说，给定解码器的当前时刻 $t^\prime$ ，我们需要对解码器中不同时刻的隐含层变量求加权平均。而权值也称注意力权重。它的计算公式是

而 $e_{t^\prime t} \in \mathbb{R}$ 的计算为：

其中函数 $a$ 有多种设计方法。在Bahanau的论文中，

其中的 $\mathbf{v}$、$\mathbf{W}_s$、$\mathbf{W}_h$ 和编码器与解码器两个循环神经网络中的各个权重和偏移项以及嵌入层参数等都是需要同时学习的模型参数。在Bahanau的论文中，编码器和解码器分别使用了门控循环单元（GRU）。

在解码器中，我们需要对GRU的设计稍作修改。假设 $\mathbf{y}_t$ 是单个输出 $y_t$ 在嵌入层的结果，例如 $y_t$ 对应的 one-hot 向量 $\mathbf{o} \in \mathbb{R}^y$ 与嵌入层参数矩阵 $\mathbf{B} \in \mathbb{R}^{y \times s}$ 的乘积 $\mathbf{o}^\top \mathbf{B}$。
假设时刻 $t^\prime$ 的背景向量为 $\mathbf{c}_{t^\prime}$ 。那么解码器在 $t^\prime$ 时刻的单个隐含层变量

其中的重置门、更新门和候选隐含状态分别为

基于 GRU 的解码器实现, 含注意力机制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class Decoder(Block):
    """含注意力机制的解码器"""
    def __init__(self, hidden_dim, output_dim, num_layers, max_seq_len,
                 drop_prob, alignment_dim, encoder_hidden_dim):
        super(Decoder, self).__init__()
        self.max_seq_len = max_seq_len
        self.encoder_hidden_dim = encoder_hidden_dim
        self.hidden_size = hidden_dim
        self.num_layers = num_layers
        with self.name_scope():
            self.embedding = nn.Embedding(output_dim, hidden_dim)
            self.dropout = nn.Dropout(drop_prob)
            # 注意力机制。
            self.attention = nn.Sequential()
            with self.attention.name_scope():
                self.attention.add(nn.Dense(
                    alignment_dim, in_units=hidden_dim + encoder_hidden_dim,
                    activation="tanh", flatten=False))
                self.attention.add(nn.Dense(1, in_units=alignment_dim,
                                            flatten=False))

            self.rnn = rnn.GRU(hidden_dim, num_layers, dropout=drop_prob,
                               input_size=hidden_dim)
            self.out = nn.Dense(output_dim, in_units=hidden_dim)
            self.rnn_concat_input = nn.Dense(
                hidden_dim, in_units=hidden_dim + encoder_hidden_dim,
                flatten=False)

    def forward(self, cur_input, state, encoder_outputs):
        # 当RNN为多层时，取最靠近输出层的单层隐含状态。
        single_layer_state = [state[0][-1].expand_dims(0)]
        encoder_outputs = encoder_outputs.reshape((self.max_seq_len, 1,
                                                   self.encoder_hidden_dim))
        # single_layer_state尺寸: [(1, 1, decoder_hidden_dim)]
        # hidden_broadcast尺寸: (max_seq_len, 1, decoder_hidden_dim)
        hidden_broadcast = nd.broadcast_axis(single_layer_state[0], axis=0,
                                             size=self.max_seq_len)

        # encoder_outputs_and_hiddens尺寸:
        # (max_seq_len, 1, encoder_hidden_dim + decoder_hidden_dim)
        encoder_outputs_and_hiddens = nd.concat(encoder_outputs,
                                                hidden_broadcast, dim=2)

        # energy尺寸: (max_seq_len, 1, 1)
        energy = self.attention(encoder_outputs_and_hiddens)

        batch_attention = nd.softmax(energy, axis=0).reshape(
            (1, 1, self.max_seq_len))

        # batch_encoder_outputs尺寸: (1, max_seq_len, encoder_hidden_dim)
        batch_encoder_outputs = encoder_outputs.swapaxes(0, 1)

        # decoder_context尺寸: (1, 1, encoder_hidden_dim)
        decoder_context = nd.batch_dot(batch_attention, batch_encoder_outputs)

        # input_and_context尺寸: (1, 1, encoder_hidden_dim + decoder_hidden_dim)
        input_and_context = nd.concat(self.embedding(cur_input).reshape(
            (1, 1, self.hidden_size)), decoder_context, dim=2)
        # concat_input尺寸: (1, 1, decoder_hidden_dim)
        concat_input = self.rnn_concat_input(input_and_context)
        concat_input = self.dropout(concat_input)

        # 当RNN为多层时，用单层隐含状态初始化各个层的隐含状态。
        state = [nd.broadcast_axis(single_layer_state[0], axis=0,
                                   size=self.num_layers)]

        output, state = self.rnn(concat_input, state)
        output = self.dropout(output)
        output = self.out(output)
        # output尺寸: (1, output_size)，hidden尺寸: [(1, 1, decoder_hidden_dim)]
        return output, state

    def begin_state(self, *args, **kwargs):
        return self.rnn.begin_state(*args, **kwargs)

为了初始化解码器的隐含状态，我们通过一层全连接网络来转化编码器的输出隐含状态
1
2
3
4
5
6
7
8
9
10
11
class DecoderInitState(Block):
    """解码器隐含状态的初始化"""
    def __init__(self, encoder_hidden_dim, decoder_hidden_dim):
        super(DecoderInitState, self).__init__()
        with self.name_scope():
            self.dense = nn.Dense(decoder_hidden_dim,
                                  in_units=encoder_hidden_dim,
                                  activation="tanh", flatten=False)

    def forward(self, encoder_state):
        return [self.dense(encoder_state)]

束搜索

上文我们提到编码器最终输出了一个背景向量 $\mathbf{c}$，该背景向量编码了输入序列 $x_1, x_2, \ldots, x_T$ 的信息。假设训练数据中的输出序列是 $y_1, y_2, \ldots, y_{T^\prime}$，输出序列的生成概率是

对于机器翻译的输出来说，如果输出语言的词汇集合 $\mathcal{Y}$ 的大小为 $|\mathcal{Y}|$，输出序列的长度为 $T^\prime$，那么可能的输出序列种类是 $\mathcal{O}(|\mathcal{Y}|^{T^\prime})$。为了找到生成概率最大的输出序列，一种方法是计算所有 $\mathcal{O}(|\mathcal{Y}|^{T^\prime})$ 种可能序列的生成概率，并输出概率最大的序列。我们将该序列称为最优序列。但是这种方法的计算开销过高（例如，$10000^{10} = 1 \times 10^{40}$）。

我们目前所介绍的解码器在每个时刻只输出生成概率最大的一个词汇。对于任一时刻 $t^\prime$，我们从 $|\mathcal{Y}|$ 个词中搜索出输出词

因此，搜索计算开销（ $\mathcal{O}(|\mathcal{Y}| \times {T^\prime})$ ）显著下降（例如，$10000 \times 10 = 1 \times 10^5$），但这并不能保证一定搜索到最优序列。

束搜索（beam search） 介于上面二者之间。我们来看一个例子。

假设输出序列的词典中只包含五个词：$\mathcal{Y} = \{A, B, C, D, E\}$。束搜索的一个超参数叫做 束宽（beam width）。以束宽等于 2 为例，假设输出序列长度为 3，假如时刻 1 生成概率 $\mathbb{P}(y_{t^\prime} \mid \mathbf{c})$ 最大的两个词为 $A$ 和 $C$ ，我们在时刻 2 对于所有的 $y_2 \in \mathcal{Y}$ 都分别计算 $\mathbb{P}(y_2 \mid A, \mathbf{c})$ 和 $\mathbb{P}(y_2 \mid C, \mathbf{c})$ ，从计算出的 10 个概率中取最大的两个，假设为 $\mathbb{P}(B \mid A, \mathbf{c})$ 和 $\mathbb{P}(E \mid C, \mathbf{c})$ 。那么，我们在时刻 3 对于所有的 $y_3 \in \mathcal{Y}$ 都分别计算 $\mathbb{P}(y_3 \mid A, B, \mathbf{c})$ 和 $\mathbb{P}(y_3 \mid C, E, \mathbf{c})$ ，从计算出的 10 个概率中取最大的两个，假设为 $\mathbb{P}(D \mid A, B, \mathbf{c})$ 和 $\mathbb{P}(D \mid C, E, \mathbf{c})$。

接下来，我们可以在输出序列：$A$、$C$、$AB$、$CE$、$ABD$、$CED$ 中筛选出以特殊字符 EOS 结尾的候选序列。再在候选序列中取以下分数最高的序列作为最终候选序列：

其中 $L$ 为候选序列长度，$\alpha$ 一般可选为 0.75。分母上的 $L^\alpha$ 是为了惩罚较长序列的分数中的对数相加项。

评价翻译结果

2002 年，IBM 团队提出了一种评价翻译结果的指标，叫做 BLEU （Bilingual Evaluation Understudy）。

设 $k$ 为我们希望评价的 n-gram 的最大长度，例如 $k=4$ 。n-gram 的精度 $p_n$ 为模型输出中的 $n-gram$ 匹配参考输出的数量与模型输出中的 n-gram 的数量的比值。例如，参考输出（真实值）为 ABCDEF，模型输出为 ABBCD。那么 $p_1 = 4/5, p_2 = 3/4, p_3 = 1/3, p_4 = 0$。设 $len_{ref}$ 和 $len_{MT}$ 分别为参考输出和模型输出的词数。那么，BLEU 的定义为

需要注意的是，随着 $n$ 的提高，n-gram 的精度的权值随着 $p_n^{1/2^n}$ 中的指数减小而提高。例如 $0.5^{1/2} \approx 0.7, 0.5^{1/4} \approx 0.84, 0.5^{1/8} \approx 0.92, 0.5^{1/16} \approx 0.96$。换句话说，匹配 4-gram 比匹配 1-gram 应该得到更多奖励。另外，模型输出越短往往越容易得到较高的 n-gram 的精度。因此，BLEU 公式里连乘项前面的系数为了惩罚较短的输出。例如当 $k=2$ 时，参考输出为 ABCDEF，而模型输出为 AB，此时的 $p_1 = p_2 = 1$，而 $\exp(1-6/3) \approx 0.37$，因此 BLEU=0.37。当模型输出也为 ABCDEF 时，BLEU=1。

结论

  • 编码器-解码器（seq2seq）的输入和输出可以都是不定长序列。
  • 在解码器上应用注意力机制可以在解码器的每个时刻使用不同的背景向量。每个背景向量相当于对输入序列的不同部分分配了不同的注意力。
  • 我们可以将编码器—解码器和注意力机制应用于神经机器翻译中。
  • 束搜索有可能提高输出质量。
  • BLEU可以用来评价翻译结果。