图像语义分割的深度学习方法发展到现在,一个通用的框架基本确定了,即如下图所示:
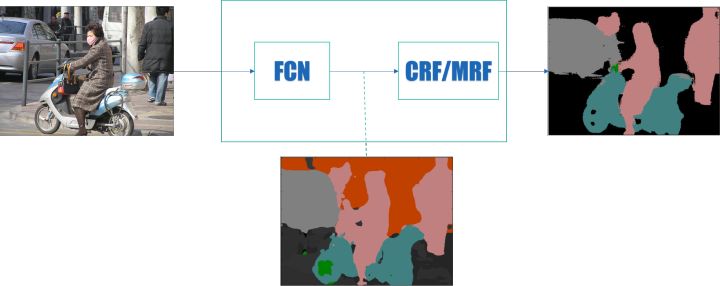
其中, FCN 表示各种全卷积网络,CRF 为条件随机场,MRF 为马尔科夫随机场
前端使用 FCN 进行特征粗提取,后端使用 CRF/MRF 优化前端的输出,最后得到分割图。在前一篇关于语义分割的总结中,我已经把前端的不同架构大致总结了,这篇主要介绍后端优化方法。
全连接条件随机场 (DenseCRF)
Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials
对于每个像素 $i$ 具有类别标签 $x_i$ 还有对应的观测值 $y_i$,这样每个像素点作为节点,像素与像素间的关系作为边,即构成了一个条件随机场。而且我们通过观测变量 $y_i$ 来推测像素 $i$ 对应的类别标签 $x_i$。条件随机场如下:
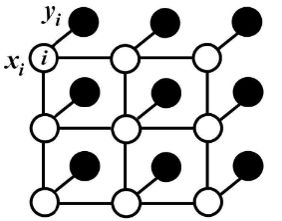
条件随机场符合吉布斯分布:(此处的 x 即上面说的观测值)
其中的 $E(\mathbf{x|I})$ 是能量函数,为了简便,以下省略全局观测 $\mathbf{I}$:
其中的一元势函数 $\sum_i{\Psi_u(x_i)}$ 即来自于前端 FCN 的输出。而二元势函数如下:
二元势函数就是描述像素点与像素点之间的关系,鼓励相似像素分配相同的标签,而相差较大的像素分配不同标签,而这个“距离”的定义与颜色值和实际相对距离有关。所以这样 CRF 能够使图片尽量在边界处分割。
而全连接条件随机场的不同就在于,二元势函数描述的是每一个像素与其他所有像素的关系,所以叫“全连接”。
CRFasRNN
最开始使用 DenseCRF 是直接加在 FCN 的输出后面,可想这样是比较粗糙的。而且在深度学习中,我们都追求 end-to-end 的系统,所以 CRFasRNN 这篇文章将 DenseCRF 真正结合进了 FCN 中。
这篇文章也使用了平均场近似的方法,因为分解的每一步都是一些相乘相加的计算,和普通的加减(具体公式还是看论文吧),所以可以方便的把每一步描述成一层类似卷积的计算。这样即可结合进神经网络中,并且前后向传播也不存在问题。
当然,这里作者还将它进行了迭代,不同次数的迭代得到的结果优化程度也不同(一般取 10 以内的迭代次数),所以文章才说是 as RNN。优化结果如下:
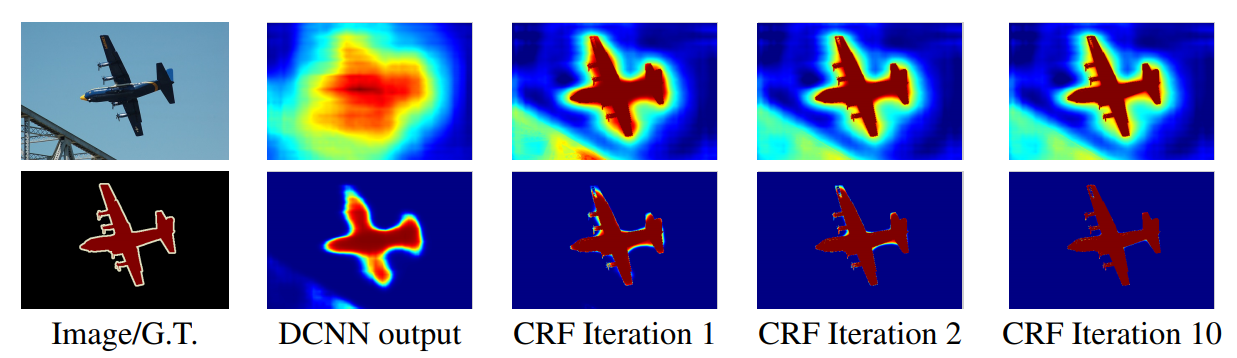
马尔科夫随机场 (MRF)
在 Deep Parsing Network 中使用的是 MRF,它的公式具体的定义和 CRF 类似,只不过作者对二元势函数进行了修改:
其中,作者加入的 $\lambda_k$ 为 label context,因为 $u_k$ 只是定义了两个像素同时出现的频率,而 $\lambda_k$ 可以对一些情况进行惩罚,比如,人可能在桌子旁边,但是在桌子下面的可能性就更小一些。所以这个量可以学习不同情况出现的概率。而原来的距离 $d(i,j)$ 只定义了两个像素间的关系,作者在这儿加入了个 triple penalty,即还引入了 $j$ 附近的 $z$,这样描述三方关系便于得到更充足的局部上下文。具体结构如下:
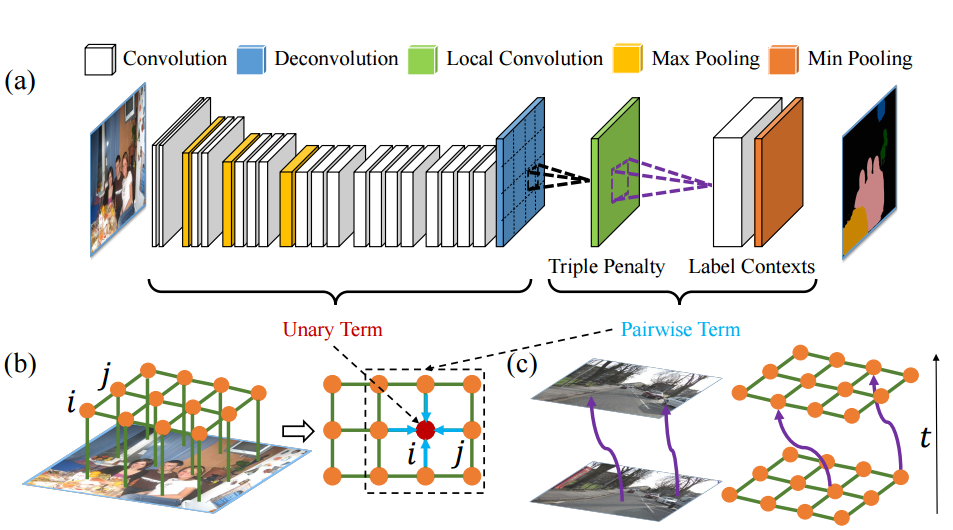
这个结构的优点在于:
- 将平均场构造成了 CNN
- 联合训练并且可以 one-pass inference,而不用迭代
高斯条件随机场(G-CRF)
Fast, Exact and Multi-Scale Inference for Semantic Image Segmentation with Deep Gaussian CRFs
这个结构使用 CNN 分别来学习一元势函数和二元势函数。这样的结构是我们更喜欢的: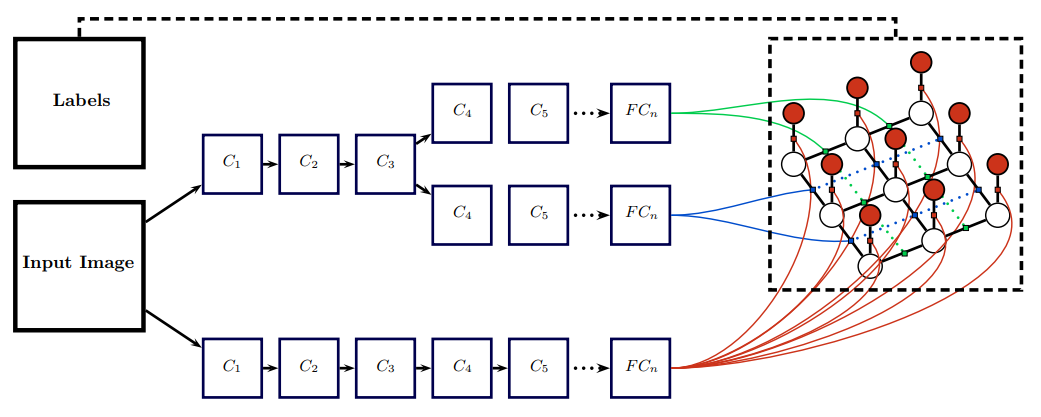
而此中的能量函数又不同于之前:
而当 $(\mathbf{A+\lambda I)}$ 是对称正定时,求 $E(\mathbf{x})$ 的最小值等于求解:
而 G-CRF 的优点在于:
- 二次能量有明确全局
- 解线性简便很多
感悟
- 深度学习+概率图模型(PGM)是一种趋势。其实 DL 说白了就是进行特征提取,而 PGM 能够从数学理论很好的解释事物本质间的联系。
- 概率图模型的网络化。因为 PGM 通常不太方便加入 DL 的模型中,将 PGM 网络化后能够使 PGM 参数自学习,同时构成 end-to-end 的系统。
参考文章:
【总结】图像语义分割之FCN和CRF